Question

How do you graph the line $x + 2y = 4$?

Answer 1

Here, we will substitute different values of $x$ and $y$ in the given equation to get corresponding values of $y$ and $x$. From this we will get coordinate points and using these points we will draw a graph.

Complete step by step solution:
The given equation is $x + 2y = 4$. We observe from this equation that the powers of $x$ and $y$ are both one. So, the given equation is a linear equation.
The graph of a linear equation is always a straight line. Let us draw the graph as follows:
Let us find two points lying on the graph of the given linear equation. The two points to be found are those that satisfy the linear equation.
Let us substitute $x = 0$ in the given equation and find the value of $y$.
$\begin{array}{l}\left( 0 \right) + 2y = 4\\\ \Rightarrow 2y = 4\end{array}$
Dividing both sides by 2, we get
$\Rightarrow y = 2$
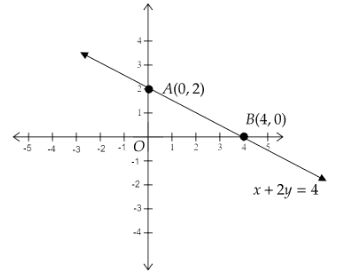
We see that when $x = 0$, we get $y = 2$. So, one of the points is $A(0,2)$.
To find another point, put $y = 0$.
$x + 2\left( 0 \right) = 4$
$\Rightarrow x = 4$
In this case, we get $x = 4$. So, the second point is $B(4,0)$.
Using these points, we will draw the graph of $x + 2y = 4$.
The point $A(0,2)$ will lie on the $y$-axis, since the $x -$coordinate is zero. The point $B(4,0)$ will lie on the $x -$axis since the $y$- coordinate is zero.
Therefore, we get the graph as follows:

Note:
Another method to draw the graph is by slope-intercept form. We shall compare the given linear equation to the slope-intercept form of a linear equation which is $y = mx + c$, where $m$is the slope of the line and $c$is the $y -$intercept, i.e., the point where the graph cuts the $y -$axis.
Let us rewrite the equation $x + 2y = 4$ as $y = 2 - \dfrac{x}{2}$.
Comparing the equation $y = 2 - \dfrac{x}{2}$ with $y = mx + c$, we get
$m = - \dfrac{1}{2}$ and $c = 2$.
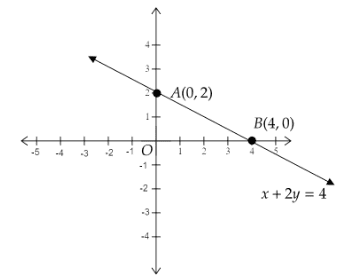
Here the slope is $- \dfrac{1}{2}$ and the $y -$intercept is $2$. So, one of the points is $A(0,2)$.
First, we have to mark the $y -$intercept. Since, the $y -$intercept is positive, i.e., $2$, it will lie on the $+ y$ axis. Now, the slope is $- \dfrac{1}{2}$ .
Here the numerator $- 1$ means we have to go 1 unit down the point $2$ and the denominator 2 means we have to go right by 2 units. So, the point we reach is $(2,1)$ which satisfies the equation $x + 2y = 4$. So, the second point is $B(4,0)$.
Therefore, we get the graph as follows: