Question

How do you graph the line that passes through the origin parallel to the line $x+y=10$?

Answer 1

First we will find the equation of the line. To do this, we will assume the required equation of the line passing through the origin in slope intercept form as $y=mx$, where m = slope. The value of m will be equal to the value of the slope of the given line $x+y=10$. Now, to find the slope of $x+y=10$ we will compare it with the general form $y=mx+c$, where c = y – intercept. Once the value of slope is found we will easily plot the graph.

Complete step by step solution:
Here, we have been asked to plot the graph of a line which passes through the origin and is parallel to the line $x+y=10$.
Now, to plot the graph first we need to determine the equation of the required line. We know that the general equation of the line in slope intercept form is given as $y=mx+c$, where m = slope and c = y – intercept. It has been given to us that the line is passing through the origin, so the y – intercept will be 0. Therefore, the equation of the line becomes,
$\Rightarrow y=mx$
Now, since the above line is parallel to the line $x+y=10$, as stated in the question, so their slopes will be equal. We can write the equation of line $x+y=10$ in slope intercept form as:
$\Rightarrow y=-x+10$
On comparing it with the general form $y=mx+c$ we get $m=-1$, so the equation of the assumed line becomes:
$\begin{aligned} & \Rightarrow y=-x \\\ & \Rightarrow x+y=0...............\left( i \right) \\\ \end{aligned}$
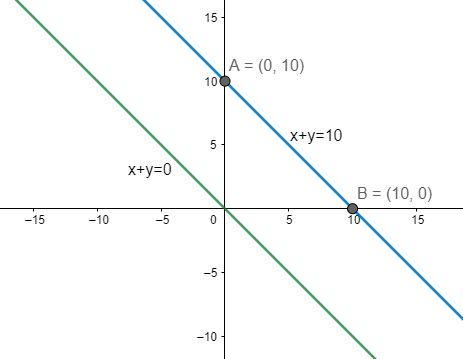
Therefore, the plot of the two lines $x+y=0$ and $x+y=10$ can be shown as below:

Note: It is necessary to determine the equation of the line because it will be difficult to draw the graph if we don’t know the equation of line. Always remember that when a line passes through the origin then its y – intercept is 0. This can be proved by considering the fact that if the line passes through the origin then it will satisfy the point O (0, 0), i.e. the origin.