Question

How do you graph the line that passes through $\left( { - 2,2} \right)$ parallel to the line whose slope is -1?

Answer 1

In this question we have to find the graph of the equation of the line which passes through the given point and parallel to the line whose slope is given, this can be done by using the fact which is, if the slopes of the lines that are parallel which are given as ${m_1}$ and ${m_2}$, then the slopes will be equal, i.e, ${m_1} = {m_2}$, by using the formula we will get the slope of the required line and then by using slope-point formula which is given by, $y - {y_1} = m\left( {x - {x_1}} \right)$, by substituting the given point and the slope and further simplification we will get the equation of the line, then graph the equation to get the required graph.

Complete step by step solution:
Given that the required equation which passes through the point $\left( { - 2,2} \right)$ and parallel to the line whose slope is -1
Now using the fact that slope of the given line, then by using the fact which is, if the slopes of the lines that are parallel which are ${m_1}$ and ${m_2}$, then of the slopes will be equal, i.e, ${m_1} = {m_2}$,
So, here ${m_1} = - 1$ and the slope of the required line is ${m_2}$, by substituting the values in the formula we get,
$\Rightarrow {m_2} = - 1$
So, the slope of the required line is $- 1$,
Now by using slope-point formula which is given by, $y - {y_1} = m\left( {x - {x_1}} \right)$, so here, point is $\left( { - 2,2} \right)$ and the slope is $- 1$,
So here ${x_1} = - 2$ and ${y_1} = 2$ and $m = - 1$, by substituting the values in the formula we get,
$\Rightarrow \left( {y - 2} \right) = - 1\left( {x - \left( { - 2} \right)} \right)$,
Now simplifying we get,
$\Rightarrow \left( {y - 2} \right) = - 1\left( {x + 2} \right)$,
Now multiplying we get,
$\Rightarrow \left( {y - 2} \right) = - x - 2$,
Now add 2 on both sides we get,
$\Rightarrow y - 2 + 2 = - x - 2 + 2$,
Now eliminating like terms we get,
$\Rightarrow y = - x$,
Now simplifying we get,
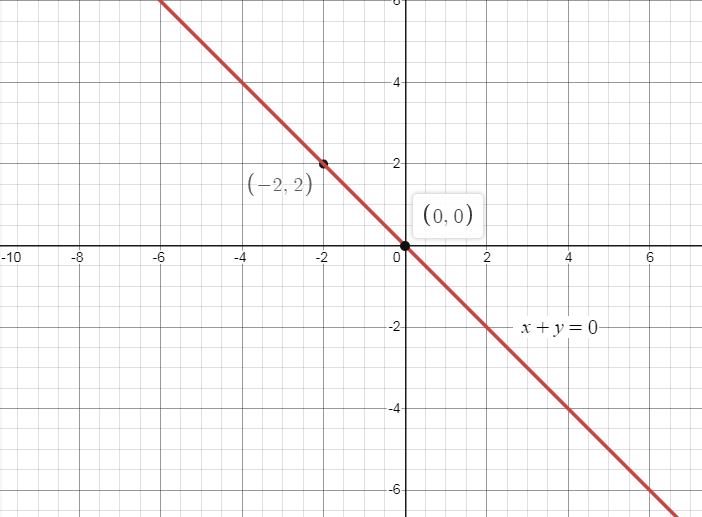
$\Rightarrow x + y = 0$,
So, the line is $x + y = 0$.
Now plotting the point and the line we got on the graph we get,

Note: Remember that if the slope of a line is equal to zero then it is parallel to x-axis and if the slope tends to infinity then it is perpendicular to x-axis. Also, we can remember that if the x-coordinates of the two points through which the line passes are same it must be perpendicular to the x-axis and y-coordinates of the two points through which the line passes are same it must be parallel to the x-axis.