Question

How do you graph the line given (2, 2) with $m=3$ ?

Answer 1

To graph the line with point (2, 2) and $m=3$ which is the slope of the line. For that, we are required to find the equation of a line. We can find the equation of a line if we know a point $\left( {{x}_{1}},{{y}_{1}} \right)$ and slope “m” is as follows: $y-{{y}_{1}}=m\left( x-{{x}_{1}} \right)$. So, we will substitute the point (2, 2) and slope $m=3$ in this equation of line. And using this equation of line we can graph the given line.

Complete step by step answer:
In the above problem, we have given a point (2, 2) and a slope of 3 of a given line. Using this point and a slope, we are going to write the equation of a line.
We know that, the equation of a line with point $\left( {{x}_{1}},{{y}_{1}} \right)$ and the slope “m” is as follows:
$\Rightarrow y-{{y}_{1}}=m\left( x-{{x}_{1}} \right)$
Substituting ${{x}_{1}}=2,{{y}_{1}}=2$ and $m=3$ in the above equation we get,
$\Rightarrow y-2=3\left( x-2 \right)$
Multiplying 3 by $\left( x-2 \right)$ in the L.H.S of the above equation we get,
$\Rightarrow y-2=3x-6$
Adding 2 on both the sides we get,
$\begin{aligned} & y-2+2=3x-6+2 \\\ & \Rightarrow y=3x-4 \\\ \end{aligned}$
Hence, we have found the equation of line as follows:
$y=3x-4$
Now, to graph this equation of line, we are going to put x as 0 in the above equation we get,
$\begin{aligned} & y=3\left( 0 \right)-4 \\\ & \Rightarrow y=-4 \\\ \end{aligned}$
From the above, we got one point as (0, -4). Now, we are going to put y as 0 in the above equation and then calculate the value of y we are getting.
$\begin{aligned} & \Rightarrow y=3x-4 \\\ & \Rightarrow 0=3x-4 \\\ \end{aligned}$
Adding 4 on both the sides we get,
$\begin{aligned} & \Rightarrow 4=3x-4+4 \\\ & \Rightarrow 4=3x \\\ \end{aligned}$
Dividing 3 on both the sides we get,
$\begin{aligned} & \Rightarrow \dfrac{4}{3}=\dfrac{3x}{3} \\\ & \Rightarrow \dfrac{4}{3}=x \\\ \end{aligned}$
From the above, the second point we get is $\left( \dfrac{4}{3},0 \right)$.
Plotting the first point i.e. (0, -4) on the graph we get,

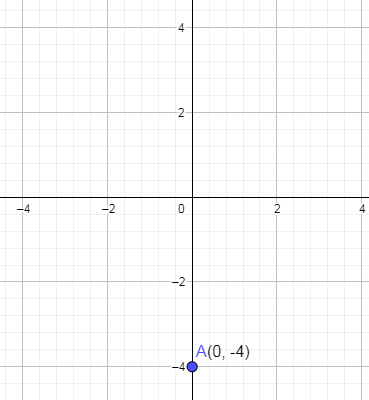
Now, plotting the second point i.e. $\left( \dfrac{4}{3},0 \right)$ which we have solved above on the graph we get,

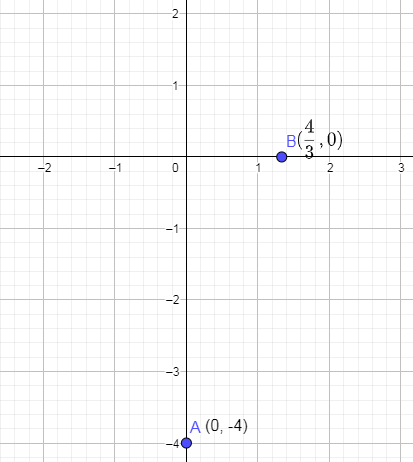
Now, we are going to join these two points on the graph to get the line given in the above problem as follows:

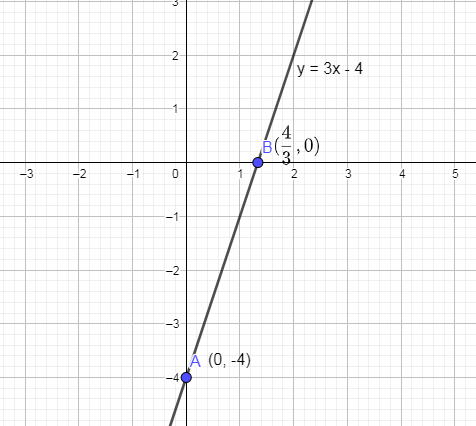
Hence, we have drawn the line passing through point (2, 2) and slope as 3.

Note: You can check the straight line you drew above on the graph is correct or not by marking a point with x axis as 2 and then draw a perpendicular from this point on the y axis and see what is the foot of the perpendicular you are getting on the y axis.
In the below figure, we have marked a point on the straight line whose x coordinate is 2.

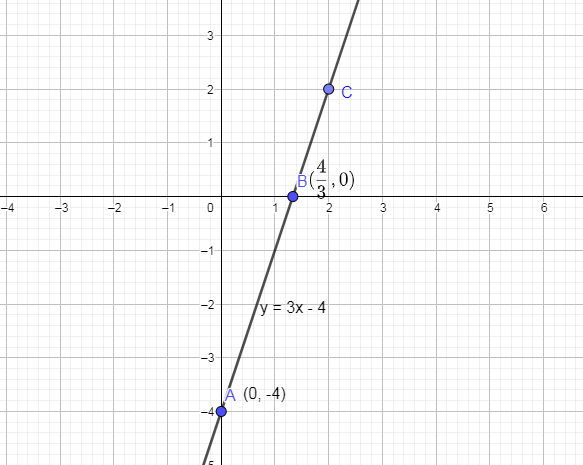
Now, we are going to drop a perpendicular from this point C on the y axis and we get,

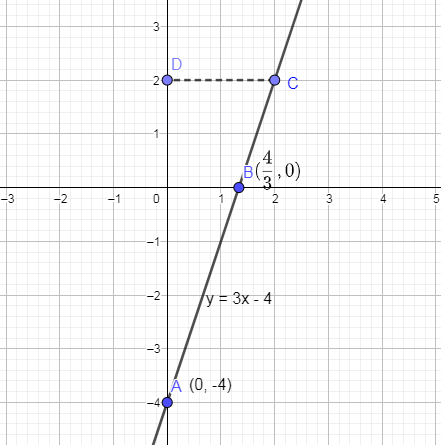
As you can see that foot of the perpendicular from point C on the y axis is point D and its value is 2. And in the above problem it is given that the line is passing through the point (2, 2) and we are getting the same point from the graph we drew. Hence, the straight line we drew is correct.