Question

How do you graph the line $2x+5y=0$?

Answer 1

Here we need to draw the graph for the given line $2x+5y=0$. For drawing the graph we will obtain two points which satisfy the line equation on substituting and plot them and join them and extend them to make a straight line.

Complete step-by-step solution:
Now from the question we have been asked to draw the graph for the given line $2x+5y=0$
For drawing the graph we will obtain two points which satisfy the line equation on substituting in the given equation.
If we substitute $x=0$ then we will have
$\begin{aligned} & \Rightarrow 2\left( 0 \right)+5y=0 \\\ & \Rightarrow 5y=0 \\\ & \Rightarrow y=0 \\\ \end{aligned}$
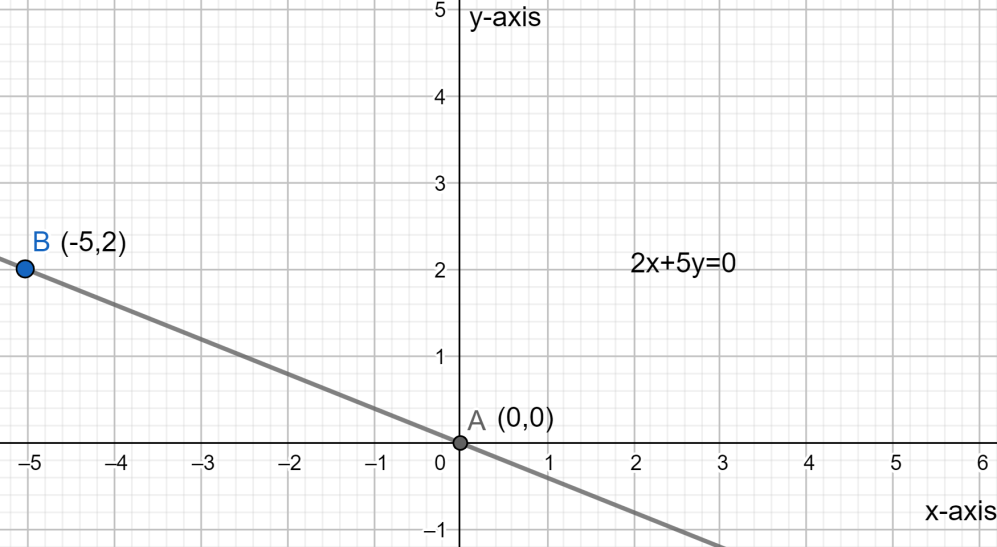
Hence $\left( 0,0 \right)$ is a point on the given straight line.
If we simplify the given equation of the straight line we can write it as $\Rightarrow 2x=-5y$ .
By observing this we will wish to substitute $x=-5$ after substituting it we will have

$\begin{aligned} & \Rightarrow 2\left( -5 \right)+5y=0 \\\ & \Rightarrow -10+5y=0 \\\ & \Rightarrow 5y=10 \\\ & \Rightarrow y=2 \\\ \end{aligned}$
Hence $\left( -5,2 \right)$ is another point which lies on the straight line.
Now we will mark these points on the graph and join them and extend the line we got as shown below.

Note: In this question we can try to plot this graph by using the slope-intercept form alternatively. The slope intercept form is defined as for any equation of the straight line in the form of $y=mx+c$ $m$ is the slope and if it is in the form of $ax+by+c=0$ then the slope is $\dfrac{-a}{b}$ and the $\text{x-intercept}$ is $\dfrac{-c}{a}$ and $\text{y-intercept}$ is $\dfrac{-c}{b}$ . Here in this question by using this method we can find only one point with which the line we had drawn may not be appropriate so we had used the substitution method.