Question

How do you graph the inequality $y\underline{>}\dfrac{3}{2}x-3$?

Answer 1

Suppose an equation of straight line to be $y=ax+b$. We can draw the graph of $y=ax+b$ from the simple graph $y=x$. We need to modify the $y=x$ graph by shifting and scaling methods. It is a better idea to modify the graph of $y=x$ in such a manner that we get the required graph by going from left side to right side of the equation $y=\dfrac{3}{2}x-3$.

Complete step by step answer:
As per the given question, we need to graph a straight line which is given by the equation $y=\dfrac{3}{2}x-3$.
A straight line can be traced out on the cartesian plane by just two points lying on it. We can also use a third point for sort of check. It is very simple to graph the $y=x$ line as it is symmetric to both x and y axes.
The graph of $y=x$ is as shown in below figure:

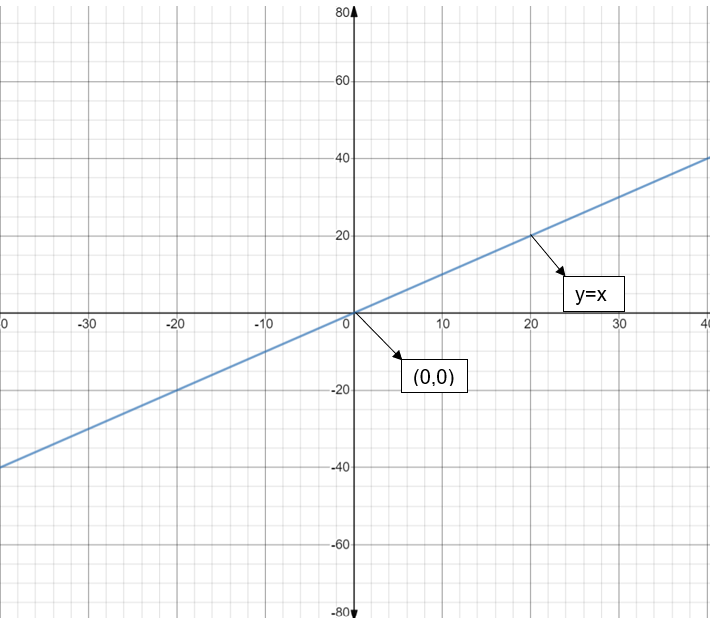
If we go from left hand side to right hand side of the equation $y=\dfrac{3}{2}x-3$, it is clear that we need to first scale the $y=x$ graph by a factor $\dfrac{3}{2}$. Then we get $y=\dfrac{3}{2}x$.
And the graph of $y=\dfrac{3}{2}x$ is as shown in the below figure:

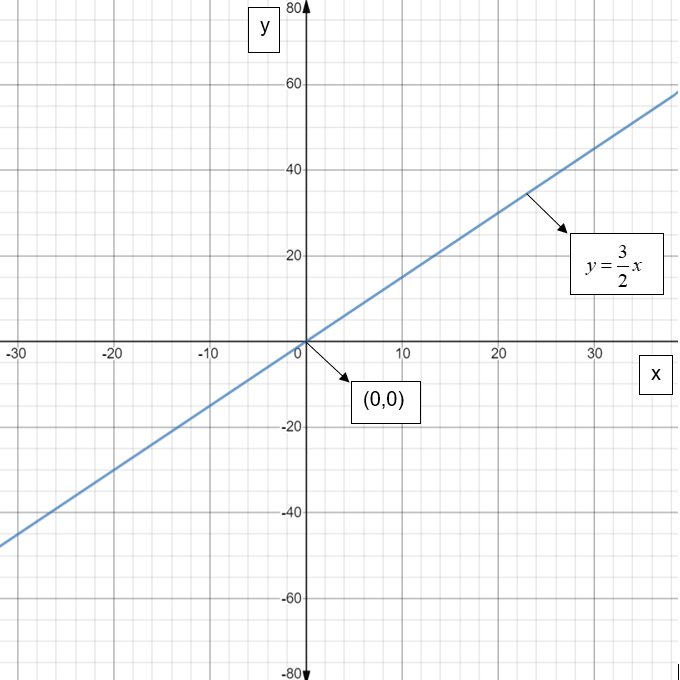
Now, we need to shift the $y=\dfrac{3}{2}x$ graph right hand side by 3 units to get the required straight line $y=\dfrac{3}{2}x-3$. And the graph of $y=\dfrac{3}{2}x-3$ is shown in the below figure:

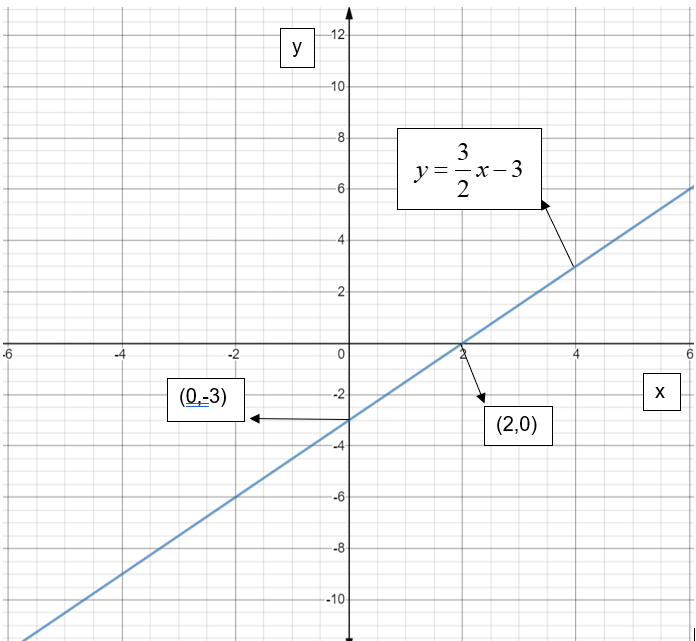
Since we need to plot $y\underline{>}\dfrac{3}{2}x-3$ we have to shade the part above the line. Thus, it looks like,

$\therefore$ we have to compress $y=x$ by $\dfrac{3}{2}$ and then shift it to the right hand side by 3 units and shade the part above the line to get the desired plot $y\underline{>}\dfrac{3}{2}x-3$.

Note:
We can trace the graph of $y\underline{>}\dfrac{3}{2}x-3$ by substitution by any two random values of x and joining the two random variables with a line. we have to check which part to be shaded depending on the sign given in the problem.