Question

How do you graph the inequality $5x + 7y \geqslant 10$ on the coordinate plane ?

Answer 1

First we need to draw the graph of the equation $5x + 7y = 10$. We use intercept form to draw the graph. That is we find the coordinate of the given equation lying on the line of x- axis, we can find this by substituting the value of ‘y’ is equal to zero (x-intercept). Similarly we can find the coordinate of the equation lying on the line of y- axis, we can find this by substituting the value of ‘x’ equal to zero (y-intercept). After drawing the graph we can check in which region the inequality satisfies.

Complete step by step answer:
Given, $5x + 7y \geqslant 10$. Now consider $5x + 7y = 10$.To find the x-intercept. That is the value of ‘x’ at$y = 0$. Substituting this in the given equation. We have,
$5x + 7(0) = 10$
$\Rightarrow 5x = 10$
Divide by 5 on both side,
$x = \dfrac{{10}}{5}$
$\Rightarrow x = 2$
Thus we have a coordinate of the equation which lies on the line of x-axis. The coordinate is $(2,0)$. To find the y-intercept. That is the value of ‘y’ at $x = 0$. Substituting this in the given equation we have,
$5(0) + 7y = 10$
$\Rightarrow 7y = 10$
Divide by 7 on both side,
$y = \dfrac{{10}}{7}$
$\Rightarrow y = 1.428$
Rounding off we have,
$y = 1.43$
Thus we have a coordinate of the equation which lies on the line of y-axis. The coordinate is $(0,1.43)$. Thus we have the coordinates $(2,0)$ and $(0,1.43)$.Let’s plot a graph for these coordinates. We take scale x-axis= 1 unit = 1 units and y-axis= 1 unit = 1 units.

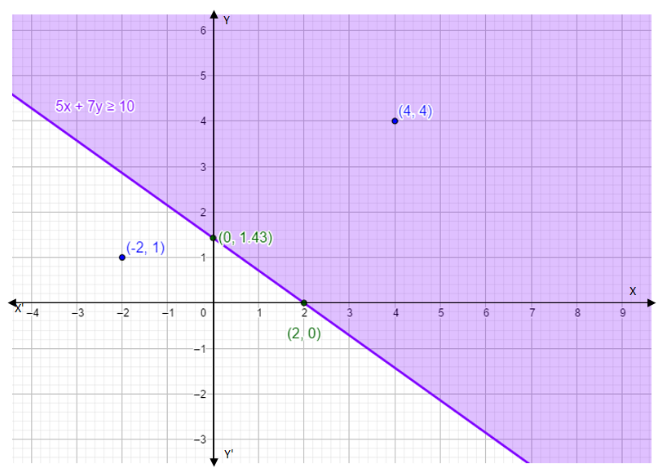
We expanded the point touching the intercepts. We took a coordinate above and below the equation of line (see in above graph).
That is $(x,y) = ( - 2,1)$ and now put it in the inequality,
$5( - 2) + 7(1) \geqslant 10$
$\Rightarrow - 10 + 7 \geqslant 10$
$\Rightarrow - 3 \geqslant 10$. Which is wrong.
Now take a coordinate above the equation of line,
That is $(x,y) = (4,4)$
$5(4) + 7(4) \geqslant 10$
$\Rightarrow 20 + 28 \geqslant 10$
$\Rightarrow 48 \geqslant 10$. Which is true.
In the above graph the shaded region is the solution of the given inequality.

Note: If we take any coordinate point below the line of the graph, the inequality satisfies. Also if we take a point on the line, the inequality will be satisfied. A graph shows the relation between two variable quantities, it contains two axes perpendicular to each other namely the x-axis and the y-axis. Each variable is measured along one of the axes. In the question, we are given one linear equation containing two variables namely x and y, x is measured along the x-axis and y is measured along the y-axis while tracing the given equations.