Question

How do you graph the given slope is $\dfrac{3}{4}$ and passes through (-1,1)?

Answer 1

In the above question, we need to plot the above line on the graph. Since, the given equation is a line where the equation of the straight line is $y = mx + c$ so we have already been given the slope and the points we can easily plot the line by joining the points and with help of slope we will be able to know the direction of the line.

Complete step by step solution:
In the above equation, we have to use the point slope method. Basically, the point-slope form is derived from the concept of finding the slope of a line when two points are given.
The point-slope form of the equation of a straight line is:
$\left( {y - {y_1}} \right) = m\left( {x - {x_1}} \right) - - (i)$
Where m is the slope of the line and the points $\left( {{x_1},{y_1}} \right)$ and $\left( {x,y} \right)$ are the points through which a straight line passes through.
Given the slope of the line $m = \dfrac{3}{4}$ Point through which given slope passes through $\left( {{x_1},{y_1}} \right) \to \left( { - 1,1} \right)$
Now we substitute the value of the given slope and the point in the equation (i), we get
$\left( {y - 1} \right) = \dfrac{3}{4}\left( {x - \left( { - 1} \right)} \right)$
By further solving the above obtained equation we get,

$$\Rightarrow 4\left( {y - 1} \right) = 3\left( {x + 1} \right) \\\ \Rightarrow 4y - 4 = 3x + 3 \\\ \Rightarrow 4y = 3x + 3 + 4 \\\ \Rightarrow 3x - 4y + 7 = 0 \\\$$

Hence we get the equation of the straight line whose slope is $m = \dfrac{3}{4}$
Now we will plot the graph of the straight line whose equation is $3x - 4y + 7 = 0$and having the slope $m = \dfrac{3}{4}$and passes through the point$\left( {{x_1},{y_1}} \right) \to \left( { - 1,1} \right)$.

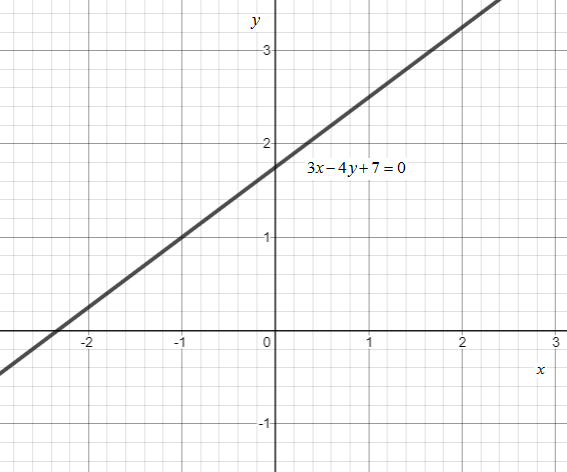
Note: An important thing to note is that slope contains the direction in which you go from one point to another. where $m = \dfrac{y}{x} \Rightarrow \dfrac{{rise}}{{run}}$.The numerator tells you much steps to go up and down and The denominator tell us how much steps to move left or right.