Question

How do you graph the function y = arctan(x)?

Answer 1

In the above question, we were asked to graph the function y = arctan(x). Also, arctan(x) is a one-to-one function. We will solve arctan(x) in the range of $-\dfrac{\pi }{2},\dfrac{\pi }{2}$ . We need to show the graph of arctan(x) as well. So, let us see how we can solve this problem.

Complete step-by-step answer:
In the given problem we have to find the function of y = arctan(x). We will note that we will be assuming a variable x which will be equal to arctan(tan(x)). So, we will create a table of typical x and tan(x) values and then we will notify the labels.

x in degrees	tan(x)	arctan(x) in degrees	x
-90	$-\infty$	-90	$-\infty$
-60	$-\sqrt{3}$	-60	$-\sqrt{3}$
-45	-1	-45	-1
-30	$-\dfrac{1}{\sqrt{3}}$	-30	$-\dfrac{1}{\sqrt{3}}$
0	0	0	0
30	$\dfrac{1}{\sqrt{3}}$	30	$\dfrac{1}{\sqrt{3}}$
45	1	45	1
60	$\sqrt{3}$	60	$\sqrt{3}$
90	$+\infty$	90	$+\infty$

Now, we will plot the arctan(x) and it should look like this.

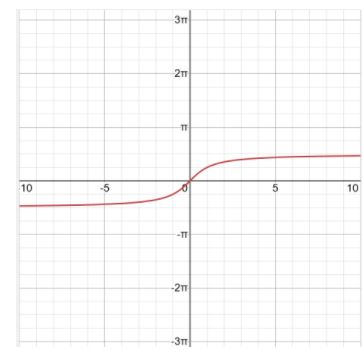
Note: In the above solution, we first find the value of arctan(x) where x = -90 to +90, and then we plot the graph for those values of arctan(x). In the graph, the y-intercept is the degree of arctan. We should note arctan(x) is a one-to-one function.