Solveeit Logo
Login

Question

Question: How do you graph the function \(y = - 3{x^2} + 2\) ?...

How do you graph the function y=−3x2+2y = - 3{x^2} + 2 ?

Explanation

Solution

For graphing the function, first we have to check the function is in standard form or not.
After attaining the standard form, we have to obtain the values from which we can ensure whether the graph opens upward or downward. After that consider x=0x = 0 and find the coordinate (x,y)\left( {x,y} \right) of the vertex. Then by equating y=0y = 0 we can find the value of xx by which we can graph the function.

Complete step by step answer:
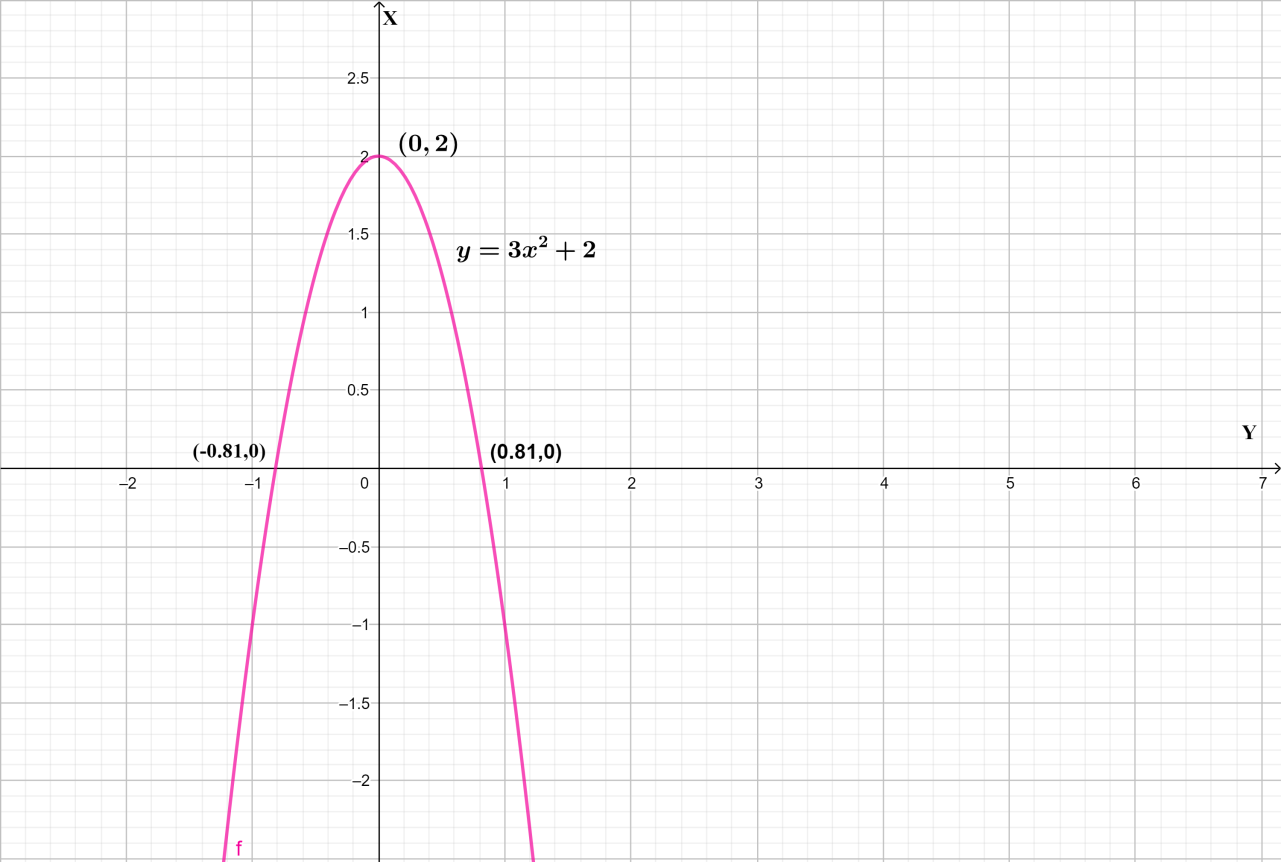
The given function is y=−3x2+2y = - 3{x^2} + 2
The equation is in the form of y=Ax2+Bx+Cy = A{x^2} + Bx + C which is in standard form.
On comparing them, we get
A=−3A = - 3 ,B=0B = 0 and C=2C = 2
Since A is negative, the graph opens downward.
Vertex is the lowest point on the graph.
The xx coordinate of the vertex occurs at −B2A\dfrac{{ - B}}{{2A}} x=(02(−3))=0x = \left( {\dfrac{0}{{2\left( { - 3} \right)}}} \right) = 0
To find the yy coordinate, we substitute x=0x = 0 and solve for y
y=(−3(0)2+2)=2y = \left( { - 3{{\left( 0 \right)}^2} + 2} \right) = 2
The vertex is at (0,2)\left( {0,2} \right) the lowest point on the graph
Now to find the xx coordinate, we can consider y=0y = 0
Therefore we get,
⇒0=(−3x2+2)\Rightarrow 0 = \left( { - 3{x^2} + 2} \right)
∴−3x2=−2\therefore - 3{x^2} = - 2
Now minus on both sides will get cancel
⇒3x2=2\Rightarrow 3{x^2} = 2
Bringing 33 to the right side, we get
⇒x2=23\Rightarrow {x^2} = \dfrac{2}{3}
Then taking the square roots we will get
⇒x=±23\Rightarrow x = \pm \sqrt {\dfrac{2}{3}}
Therefore we have two values of xx
i) x1=+23=0.81i)\,{x_1} = + \sqrt {\dfrac{2}{3}} = 0.81
ii) x2=−23=−0.81ii)\,{x_2} = - \sqrt {\dfrac{2}{3}} = - 0.81
Now by plotting the graph we get a Parabola for the function y=−3x2+2y = - 3{x^2} + 2

Note: Descriptions of graphs:

"The graph is positive"means that the yy values of the graph are positive.
"The graph is negative"means that the yy values of the graph are negative.
"The graph is increasing"means that as we move from left to right the yy values on the graph climb.
"The graph is decreasing"means that as we move from left to right the yy values on the graph drop.