Question

How do you graph the function $f\left( x \right)=-{{x}^{3}}+1$ and then use the horizontal line test to determine whether the inverse of function exists.

Answer 1

Now to draw the graph of the function we will first find the roots of the function and intercept of the function. Now we will differentiate the function and check if the function is increasing or decreasing. Also we will find the second derivative to find the concavity of the function. Hence we will draw the graph of the function. Now we will check if every horizontal line on the graph intersects the graph exactly at one point. If it does then the function is one-one function. Also we know that the function is onto and hence the function is bijective and inverse of the function exists.

Complete step by step solution:
Now first consider the given function $f\left( x \right)=-{{x}^{3}}+1$ .
Now first let us find the roots and intercept of the function.
Now to find the roots of the equation we will solve $-{{x}^{3}}+1=0$ . The equation can also be written as ${{x}^{3}}=1$ . Now we know that the roots of the equation are $1,\omega ,{{\omega }^{2}}$ . Hence the only real root is 1.
Now substituting x = 0 in the equation we get $f\left( x \right)=1$
Hence the y intercept of the function is 1.
Now let us check if the function is increasing or decreasing using the first derivative test.
Differentiating the given function we get, $f'\left( x \right)=-3{{x}^{2}}+1$ .
Now we know that ${{x}^{2}}>0$ . hence the derivative is always negative.
Hence we can say that the function is decreasing throughout.
Now let us check the second derivative.
Differentiating the function again we get,
$\Rightarrow f''\left( x \right)=-6x+1$
Now we can see that at $x=\dfrac{1}{6}$ the second derivative is 0. Also for $x>\dfrac{1}{6}$ the second derivative is negative and for $x<\dfrac{1}{6}$ the second derivative is positive.
Hence the function is concave up for $x<\dfrac{1}{6}$ and concave down for $x>\dfrac{1}{6}$ .
Now let us draw the graph of the function with all the information we have,

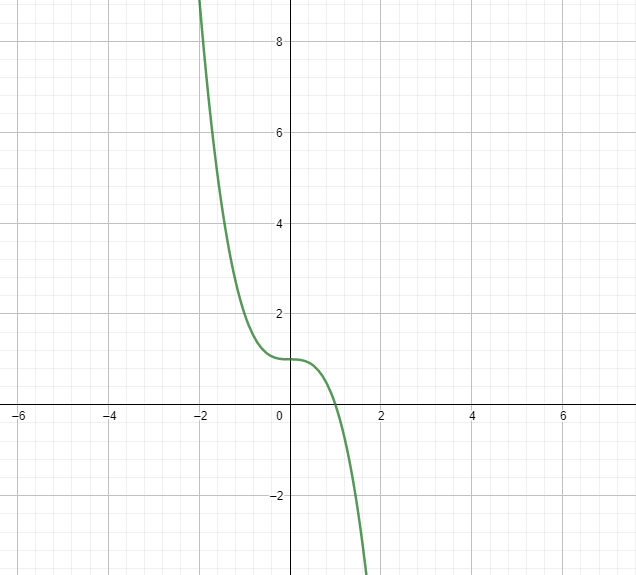
Now we can see that the function is onto.
If the function is one-one then we can say that the function is bijective.
Now we know that if all horizontal lines on a graph intersect the line exactly once then the function is one-one.
Now we can check that the horizontal lines on the graph will cut the graph exactly once.
Hence the function is one-one and hence bijective.
Now we know that the inverse of the function exists if the function is bijective.
Hence the inverse of the given function exists.

Note: Now note that if the first derivative of the function is not entirely positive or negative then we find the interval in which the function is positive and negative and hence the function is increasing and decreasing in the respective interval. Also in this case we will have an extrema where $f'\left( x \right)=0$