Question

How do you graph the function $f\left( x \right)=-4$ ?

Answer 1

Try to find the slope and y-intercept by comparing with slope intercept form i.e. $y=mx+c$. Try to plot the graph by taking different values of ‘x’ for the same value of y (since you will get a constant function so it’s ‘y’ value will be constant.)

Complete step-by-step answer:
As we know $f\left( x \right)=y$,
So, the function $f\left( x \right)$ can be written in equation form as $y=-4$
Slope intercept form: We know a general straight line has an equation in the form $y=mx+c$, where ‘m’ is the slope and ‘c’ is the intercept with the y-axis.
Now our equation $y=-4$ can be written as $y=0x+\left( -4 \right)$
So by comparing it with the slope intercept form $y=mx+c$, we get
$m=0$ and $c=-4$
Since it has a slope $=0$ so it is a constant which never changes and intercepts the y-axis at the point $-4$.
And since this is a constant function so for every value of ‘x’ there is always the same value of ‘y’ i.e. $-4$.
Now for the graph part, we have the constant value of $y=-4$ and we can take the value of x as anything say 1,2,3…
So, graph can be drawn as follows

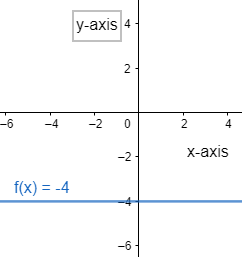
From the above graph we can conclude that $f\left( x \right)=-4$ is a straight line passing through the point $\left( 0,-4 \right)$ and parallel to the x-axis.

Note: The form of the given equation should be compared with slope point form to get the nature of the graph. Graphs should be drawn by taking different ‘x’ values for a constant ‘y’ value i.e. $-4$.