Question

How do you graph the equation $y = {(x + 1)^2} - 4$?

Answer 1

To solve this we need to give the values of ‘x’ and we can find the values of ‘y’. Otherwise we can find the coordinate of the given equation lying on the line of x- axis, we can find this by substituting the value of ‘y’ is equal to zero (x-intercept). Similarly we can find the coordinate of the equation lying on the line of y- axis, we can find this by substituting the value of ‘x’ equal to zero (y-intercept).

Complete step by step answer:
Given, $y = {(x + 1)^2} - 4$.
To find the x-intercept. That is the value of ‘x’ at$y = 0$. Substituting this in the given equation. We have,
$0 = {(x + 1)^2} - 4$
Rearranging we have,
${(x + 1)^2} = 4$
Taking square root we have,
$x + 1 = \pm 2$
$x + 1 = 2$ and $x + 1 = - 2$
$x = 2 - 1$ and $x = - 2 - 1$
$x = 1$ and $x = - 3$
Thus we have the coordinates of the equation which lies on the line of the x-axis. The coordinate are $(1,0)$and $( - 3,0)$
To find the y-intercept. That is the value of ‘y’ at $x = 0$. Substituting this in the given equation we have,
$y = {(x + 1)^2} - 4$
$\Rightarrow y = {(0 + 1)^2} - 4$
$\Rightarrow y = 1 - 4$
$\Rightarrow y = - 3$
Thus we have a coordinate of the equation which lies on the line of the y-axis. The coordinate is $(0, - 3)$.Thus we have the coordinates $(1,0)$, $( - 3,0)$ and $(0, - 3)$.
Since we have two coordinate points on the x-axis. The given equation will be curved.
So let’s find two more coordinates. Since we have $( - 3,0)$. Let's find the value of ‘y’ at x=-1
Put $x = - 1$ in $y = {(x + 1)^2} - 4$
$\Rightarrow y = {( - 1 + 1)^2} - 4$
$\Rightarrow y = - 4$
Thus we have $( - 1, - 4)$.
Put $x = - 2$ in $y = {(x + 1)^2} - 4$
$y = {( - 2 + 1)^2} - 4$
$\Rightarrow y = {( - 1)^2} - 4$
$\Rightarrow y = 1 - 4$
$\Rightarrow y = - 3$
Thus we have $( - 2, - 3)$.
Put $x = - 4$ in $y = {(x + 1)^2} - 4$
$y = {( - 4 + 1)^2} - 4$
$\Rightarrow y = {( - 3)^2} - 4$
$\Rightarrow y = 9 - 4$
$\Rightarrow y = 5$
Thus we have $( - 4,5)$.
Since we have $(1,0)$.
Put $x = 2$ in $y = {(x + 1)^2} - 4$
$y = {(2 + 1)^2} - 4$
$\Rightarrow y = {(3)^2} - 4$
$\Rightarrow y = 9 - 4$
$\Rightarrow y = 5$
Thus we have $(2,5)$.
Hence, we have the coordinates,
$(1,0)$, $( - 3,0)$,$( - 1, - 4)$ , $( - 2, - 3)$, $( - 4,5)$,$(0, - 3)$ and $(2,5)$.
Let’s plot a graph for this coordinates,

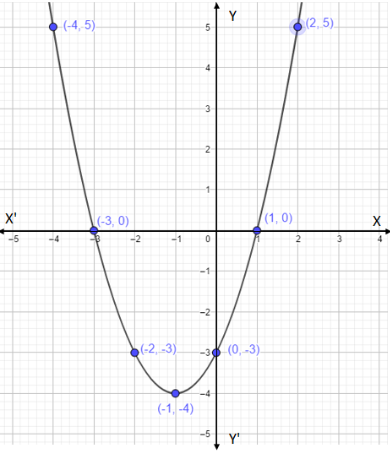
Note: Follow the same procedure for drawing the graph of any given equation. Since we have two x-intercept in the given problem, we know that it is a curve that is why we need more coordinates to draw the curve. A graph shows the relation between two variable quantities, it contains two axes perpendicular to each other namely the x-axis and the y-axis. Each variable is measured along one of the axes. In the question, we are given one linear equation containing two variables namely x and y, x is measured along the x-axis and y is measured along the y-axis while tracing the given equations.