Question

How do you graph the equation $y=8x$ by making a table and what is its domain and range?

Answer 1

We recall domain, range and graph of a function. We take five inputs $x=-2,-1,0,1,2$ to and find the corresponding outputs $y$ to make the table. We join the points $\left( x,y \right)$ to get the graph. We see if there are any points where we cannot find output and exclude it to get the domain. We find the collections of outputs to find the range.

Complete step by step solution:
We know that the domain a function $f$ is the set where it takes inputs and range co-domain is the set where it maps the inputs outputs. The set of outputs is called range. If $x$ is the variable which assigns the inputs and $y$ is the variable which assigned to outputs then we have
$y=f\left( x \right)$
We also know that the set of collection of points $\left( x,y \right)=\left( x,f\left( x \right) \right)$ is called graph of the function $f$ and the locus traced by such points is called curve of $f$. We are given in the question the following equation
$y=8x$
So the function is $f\left( x \right)=8x$. We take points from the real number set $x=-2,-1,0,1,2$ and find the corresponding outputs $y$ and the points $\left( x,y \right)$ in table.

$x$	$y=8x$	$\left( x,y \right)$
$-2$	$8\times \left( -2 \right)=-16$	$\left( -2,-16 \right)$
$-1$	$8\times \left( -1 \right)=8$	$\left( -1,-8 \right)$
0	$8\times 0=0$	$\left( 0,0 \right)$
1	$8\times 1=8$	$\left( 1,8 \right)$
2	$8\times 2=16$	$\left( 2,16 \right)$

We plot the above obtained points and join them to get the curve for $y=8x$. $$$$

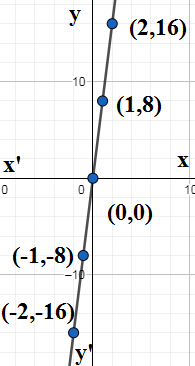
We see that for every real number $x$ we get a real number $y$ which 8 times $x$. So $f\left( x \right)=8x$ can take very real number as input and hence the domain of $f\left( x \right)$ is real number set $\mathsf{\mathbb{R}}$.We know that multiplication is closed under real number set . Since both 8 and $x$ are real numbers $8x$ is real number and hence all the outputs are real numbers. So the range of $f\left( x \right)$ is also $\mathsf{\mathbb{R}}$.

Note: We note that the line passing through the origin has the equation $y=mx$ where $m$ is the slope of the equation like the given equation $y=8x$. We also note that if for every $y$ in the range there exist only $x$ in the domain then we can define as inverse function ${{f}^{-1}}\left( x \right)$ as ${{f}^{-1}}\left( y \right)=x$. Here the inverse of $f\left( x \right)=8x$ is ${{f}^{-1}}\left( x \right)=\dfrac{1}{8}x$. We note that curves of $f,{{f}^{-1}}$ are reflections of each other about the line $y=x$.