Question

How do you graph the equation $y = - 4$ by making a table and what is its domain and range?

Answer 1

Here, the value of $y$ is constant, so we will select some arbitrary values of $x$ to find the different coordinate points. To do this, we will make a table consisting of values of $x$ and corresponding values of $y$. Then, we will draw the graph of the equation using the points and then find the domain and range.

Complete step by step solution:
The equation given to us is $y = - 4$. We have to graph this equation and find its domain and range. Let us assume $f(x) = y = - 4$.
Let us take $x = 0$. We get $y = - 4$.
If we take $x = - 4$, we get $y = - 4$ again. So, no matter what value of $x$ we take, we will always get the value of $y$ as $y = - 4$. Let us form a table and graph the equation $y = - 4$ using the table.

$x$	$f(x) = y$
$-4$	$- 4$
0	$- 4$
3	$- 4$

So, we get the points as $A( - 4, - 4)$, $B(0, - 4)$ and $C(3, - 4)$. Now we will draw the graph by plotting these points
We get the graph as follows:

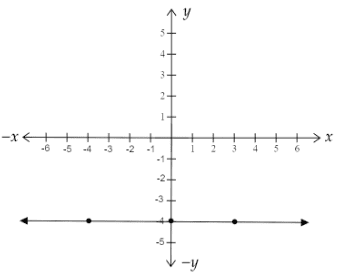
We can see from the above graph that the graph of $f(x)$ is a horizontal line passing through the point $y = - 4$. This is because the function $f$ is a constant function.
Now, let us find the domain and range of the function $f$.
The domain of a function $f$ is the set of all inputs of the function. In the given function, we consider all real numbers as inputs. So, the domain is the entire real line $\mathbb{R} = ( - \infty ,\infty )$
The range of a function $f$ is the set of all outputs of the function. In the given function, we have only one output which is $- 4$. So, the range is $\\{ - 4\\}$.

Note:
A constant function is defined a function $f:\mathbb{R} \to \mathbb{R}$, where $f(x) = c$, for all $x \in \mathbb{R}$ and $c$ is a constant. The graph of a constant function will be a line parallel to the $x -$axis. It lies above the $x -$ axis if $c$ is positive, below the $x -$ axis if $c$ is negative and coincident with the $x -$ axis if $c$ is zero. In the given problem, $c = - 4$ which is negative and so, we get a line below the $x -$ axis.