Question

How do you graph the equation $y - 2 = 3\left( {x - 1} \right)$ ?

Answer 1

Here, the given equation is an equation of the straight line. We will first write it in slope in the slope-intercept form and compare it by general slope-intercept form. So from there, we will get the value of the slope of the line and then the $y$ intercept. Then we will find the value of the $x$ intercepts by putting the value of $y$ as zero. Then using the slope and the intercepts, we will draw the graph accordingly.

Complete step by step solution:
Here we need to find the graph for the given equation and the given equation is $y - 2 = 3\left( {x - 1} \right)$.
Now, we will write it in standard form. We will use the distributive property in the right-hand side expression.
$\Rightarrow y - 2 = 3x - 3$
Now, we will add 2 on both sides. Therefore, we get
$\begin{array}{l} \Rightarrow y - 2 + 2 = 3x - 3 + 2\\\ \Rightarrow y = 3x - 1\end{array}$
We know that this is an equation of straight line and the given equation is written in the slope intercept form.
We know that the slope-intercept form of an equation is given by$y = mx + b$, where $m$ is the slope of the line and $b$ is the $y$ intercept.
Now, we will compare this equation with the given equation.
Slope in this case is $3$ and $y$ intercept is equal to $- 1$.
Now, we will find the $x$ intercepts by putting the value of $y$ as zero in $y = 3x - 1$. Therefore, we get
$0 = 3x - 1$
Now, adding 1 on both sides, we get
$\Rightarrow 0 + 1 = 3x - 1 + 1$
$\Rightarrow 1 = 3x$
Now, dividing both sides by 3, we get
$\Rightarrow \dfrac{1}{3} = \dfrac{{3x}}{3}$
On further simplification, we get
$\begin{array}{l} \Rightarrow \dfrac{1}{3} = x\\\ \Rightarrow x = \dfrac{1}{3}\end{array}$
Therefore, the $x$ intercept is equal to $\dfrac{1}{3}$.
Now, we will draw the graph using the slope and the intercepts.

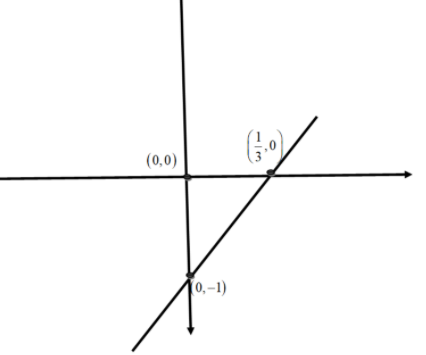
Note:
A coordinate plane is a two-dimensional number line where the vertical line is called the $y$-axis and the horizontal is called the $x$-axis. These lines are perpendicular and intersect at their zero points. Their intersection point is called the origin and usually denoted as $O$.
The slope of a line is defined as the value which measures the steepness of the line or the inclination of the line with the $x$ axis. A slope of any line can either be a positive number, negative number, zero, or undefined. As we have discussed, the slope of a vertical line that is parallel to the $y$ axis is undefined. Similarly, the slope of a horizontal line that is parallel to the axis is zero.