Question

How do you graph the equation $- 4x + 2y = 8$?

Answer 1

First of all this is a very simple and a very easy problem. The general equation of a straight line is $y = mx + c$, where $m$ is the gradient and $y = c$ is the value where the line cuts the y-axis. The number $c$ is called the intercept on the y-axis. Based on this provided information we try to find the graph of the given straight line.

Complete step by step answer: Consider the given linear equation, as given below:
$\Rightarrow - 4x + 2y = 8$
Now converting the given straight line to the standard form of the general equation of a straight line.
The general equation of a straight line is given by:
$\Rightarrow 2y = 4x + 8$
Divide the equation by 2, as shown below:
$\Rightarrow y = 2x + 4$
The slope of the straight line $y = 2x + 4$, on comparing with the straight line $y = mx + c$,
Here the slope is $m$, and here on comparing the coefficients of $x$,
$\Rightarrow m = 2$
So the slope of the given straight line $y = 2x + 4$ is $2$.
Now finding the intercept of the line $y = 2x + 4$, on comparing with the straight line $y = mx + c$, Here the intercept is $c$, and here on comparing the constants of the straight lines,
$\Rightarrow c = 4$
So the intercept of the given straight line $y = 2x + 4$ is 4.
Now plotting the straight line with slope 2 and a y-intercept of 4, as shown below:

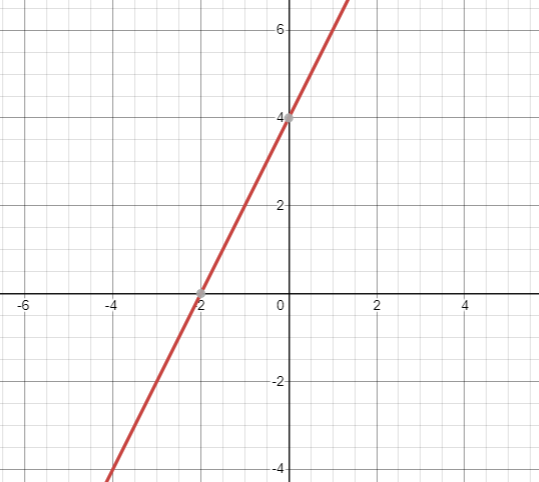
Note:
Please note that while solving such kind of problems, we should understand that if the y-intercept value is zero, then the straight line is passing through the origin, which is in the equation of $y = mx + c$, if $c = 0$, then the equation becomes $y = mx$, and this line passes through the origin, whether the slope is positive or negative.