Question

How do you graph the ellipse $\dfrac{{{x}^{2}}}{169}+\dfrac{{{y}^{2}}}{25}=1$ and find the center, the major and minor axis, vertices, foci and eccentricity?

Answer 1

In this we have been asked to draw the graph of the given ellipse $\dfrac{{{x}^{2}}}{169}+\dfrac{{{y}^{2}}}{25}=1$ and find the center, the major and minor axis, vertices, foci and eccentricity. We know that the general equation of ellipse is given as $\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$ where $a>b$ then its center is located at $\left( 0,0 \right)$ , the length of the major and minor axis is given as $2a$ and $2b$ respectively. Vertices on the major and minor axis are $\left( \pm a,0 \right)$ and $\left( 0,\pm b \right)$ . The eccentricity is given as $e=\sqrt{1-\dfrac{{{b}^{2}}}{{{a}^{2}}}}$ .

Complete step-by-step solution:
Now considering from the question we have been asked to draw the graph of the given ellipse $\dfrac{{{x}^{2}}}{169}+\dfrac{{{y}^{2}}}{25}=1$ and find the center, the major and minor axis, vertices, foci and eccentricity.
From the basic concepts we know that the general equation of ellipse is given as $\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$ where $a>b$ then its center is located at $\left( 0,0 \right)$ , the length of the major and minor axis is given as $2a$ and $2b$ respectively. Vertices on the major and minor axis are $\left( \pm a,0 \right)$ and $\left( 0,\pm b \right)$ . The eccentricity is given as $e=\sqrt{1-\dfrac{{{b}^{2}}}{{{a}^{2}}}}$ . The foci of an ellipse are given as $\left( \pm ae,0 \right)$
Here the values are $a=13,b=5$ .
Hence the center is located at $\left( 0,0 \right)$ . The vertices on the major and minor axis are $\left( \pm 13,0 \right),\left( 0,\pm 5 \right)$ respectively. The length of major and minor axis is $26,10$ respectively. The eccentricity of the given ellipse is
$\begin{aligned} & \Rightarrow e=\sqrt{1-\dfrac{{{\left( 5 \right)}^{2}}}{{{\left( 13 \right)}^{2}}}} \\\ & \Rightarrow e=\sqrt{\dfrac{{{13}^{2}}-{{5}^{2}}}{{{13}^{2}}}} \\\ & \Rightarrow e=\sqrt{\dfrac{169-25}{169}} \\\ & \Rightarrow e=\sqrt{\dfrac{144}{169}}\Rightarrow e=\dfrac{12}{13} \\\ \end{aligned}$
The foci of the given ellipse are given as
$\begin{aligned} & \left( \pm \left( 13\times \dfrac{12}{13} \right),0 \right) \\\ & \Rightarrow \left( \pm 12,0 \right) \\\ \end{aligned}$ .
The graph of the given ellipse will look like:

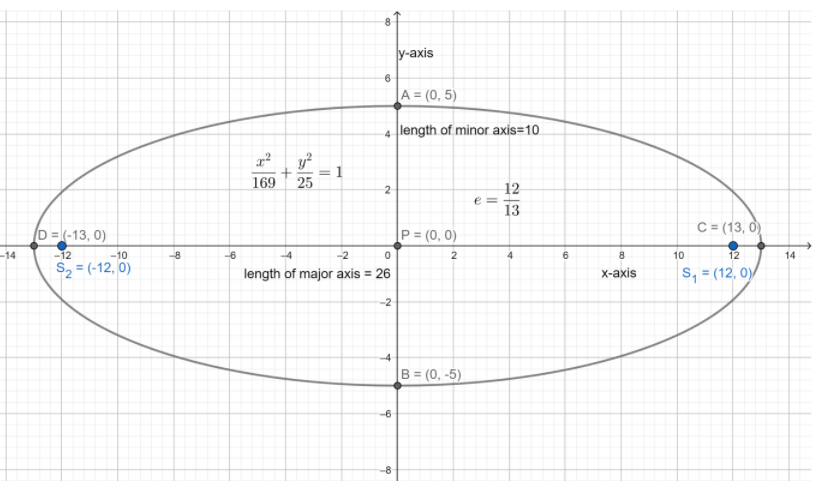
Note: While answering questions of this type we should be careful with our concepts. We should carefully mark the points on the graph and join them for getting an accurate one. Someone can make mistake during calculation and write the value of eccentricity as $\begin{aligned} & \Rightarrow e=\sqrt{1-\dfrac{{{\left( 5 \right)}^{2}}}{{{\left( 13 \right)}^{2}}}} \\\ & \Rightarrow e=\sqrt{\dfrac{169-25}{169}} \\\ & \Rightarrow e=\sqrt{\dfrac{121}{169}}\Rightarrow e=\dfrac{11}{13} \\\ \end{aligned}$
which will lead us to end up having a wrong conclusion.