Question

How do you graph the ellipse $\dfrac{{{\left( x+2 \right)}^{2}}}{16}+\dfrac{{{\left( y-5 \right)}^{2}}}{20}=1$ and find the center, the major and minor axis, vertices, foci and eccentricity?

Answer 1

In this question we have been asked to find the center, the major and minor axis, vertices, foci and eccentricity of the given ellipse $\dfrac{{{\left( x+2 \right)}^{2}}}{16}+\dfrac{{{\left( y-5 \right)}^{2}}}{20}=1$. We know that the general form of an ellipse is $\dfrac{{{\left( x-h \right)}^{2}}}{{{a}^{2}}}+\dfrac{{{\left( y-k \right)}^{2}}}{{{b}^{2}}}=1$ , where $\left( h,k \right)$ is the center of the ellipse, the major axis is given by $2a$ and the minor axis is given by $2b$, the vertices are $\left( h\pm a,k \right)$ and $\left( h,k\pm b \right)$, eccentricity $e=\sqrt{1-\dfrac{{{a}^{2}}}{{{b}^{2}}}}$ and the foci are $\left( h,k\pm be \right)$.

Complete step-by-step solution:
We have the ellipse given to us as:
$\Rightarrow \dfrac{{{\left( x+2 \right)}^{2}}}{16}+\dfrac{{{\left( y-5 \right)}^{2}}}{20}=1$
We can write the term $16={{4}^{2}}$ and $20=2\sqrt{5}$ therefore, on substituting, we get:
$\Rightarrow \dfrac{{{\left( x+2 \right)}^{2}}}{{{4}^{2}}}+\dfrac{{{\left( y-5 \right)}^{2}}}{{{\left( 2\sqrt{5} \right)}^{2}}}=1$ which is in the general form $\dfrac{{{\left( x-h \right)}^{2}}}{{{a}^{2}}}+\dfrac{{{\left( y-k \right)}^{2}}}{{{b}^{2}}}=1$.
The center is given as $\left( h,k \right)$ which is $\left( -2,5 \right)$.
The major axis will be:
$\Rightarrow 2b=2\times 2\sqrt{5}=4\sqrt{5}$
Now the minor axis will be:
$\Rightarrow 2a=2\times 4=8$
The vertices are $\left( h\pm a,k \right)$ and $\left( h,k\pm b \right)$ therefore, on substituting, we get:
$\Rightarrow \left( -2\pm 4,5 \right)$ and $\left( -2,5\pm 4\sqrt{5} \right)$
The eccentricity is given by: $e=\sqrt{1-\dfrac{{{a}^{2}}}{{{b}^{2}}}}$.
On substituting the values, we get:
$e=\sqrt{1-\dfrac{{{4}^{2}}}{{{\left( 4\sqrt{5} \right)}^{2}}}}$
On simplifying the roots, we get:
$e=\sqrt{1-\dfrac{16}{20}}$
On taking the lowest common multiple, we get:
$e=\sqrt{\dfrac{20-16}{20}}$
On simplifying, we get:
$e=\sqrt{\dfrac{4}{20}}$
On simplifying, we get:
$e=\sqrt{\dfrac{1}{5}}$
Which can be written as:
$e=\dfrac{1}{\sqrt{5}}$
The foci are $\left( h,k\pm be \right)$
On substituting the values, we get:
$\Rightarrow \left( -2,5\pm \left( 2\sqrt{5}\times \dfrac{1}{\sqrt{5}} \right) \right)$
Which can be simplified and written as:
$\Rightarrow \left( -2,5\pm 2 \right)$
Which are $\left( -2,7 \right)$ and $\left( -2,3 \right)$.
On drawing the ellipse on the graph, we get:

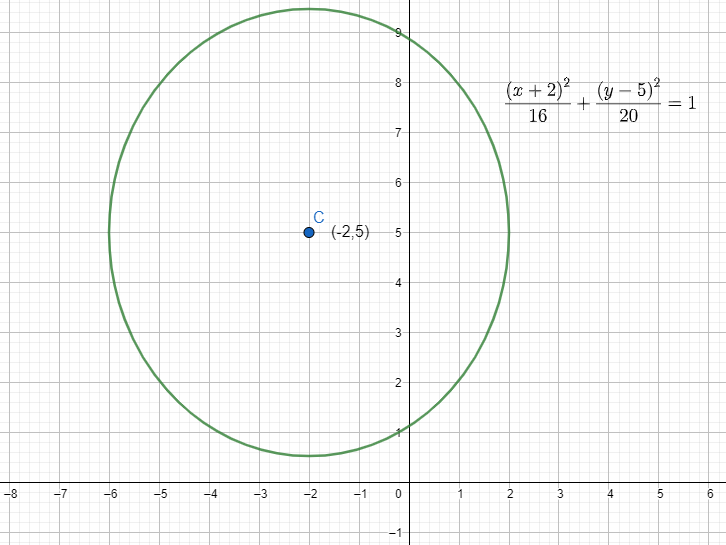
Note: The major axis of the ellipse represents the axis which is longer, in this case the $y$ axis and the minor axis represents the axis which is smaller, in this case the $x$ axis. $b$ represents the major axis and $a$ represents the minor axis. It is to be noted that in this case we have with us a vertical ellipse since $b>a$. If $a