Question

How do you graph the ellipse $36{x^2} + 9{y^2} = 324$ ?

Answer 1

Hint : An ellipse is the locus of all those points in a plane such that the sum of their distances from two fixed points in the plane, is constant. To graph the ellipse, we need to use the formula of hyperbola, such that we need the equation in a simplified form since the standard form must be equal to 1.
Formula used:
I. $\dfrac{{{{\left( {x - h} \right)}^2}}}{{{b^2}}} + \dfrac{{{{\left( {y - k} \right)}^2}}}{{{a^2}}} = 1$
II. ${a^2} - {b^2} = {c^2}$

Complete step by step solution:
Let us write the given equation:
$36{x^2} + 9{y^2} = 324$
We know the formula for equation of vertical hyperbola is:
$\dfrac{{{{\left( {x - h} \right)}^2}}}{{{b^2}}} + \dfrac{{{{\left( {y - k} \right)}^2}}}{{{a^2}}} = 1$ ………………….. 1
We need the given equation in a more simplified form since the standard form must be equal to 1, hence we have:
$\dfrac{{36{x^2}}}{{324}} + \dfrac{{9{y^2}}}{{324}} = \dfrac{{324}}{{324}}$
Simplifying the terms, we get:
$\Rightarrow \dfrac{{{x^2}}}{9} + \dfrac{{{y^2}}}{{36}} = 1$ ………………………. 2
For instance, the center is $\left( {0,0} \right)$ since there are no h or k values. Our ellipse is vertical since the highest denominator is under ${y^2}$ and our a, b, and c values can also be found.
Hence, from equation 1; formula, we get $a = 6$ and $b = 3$ from the obtained equation 2, but we need the value of c also, hence we can find it using ${a^2} - {b^2} = {c^2}$ i.e.,
${a^2} - {b^2} = {c^2}$
Substitute the values of a and b as:
$\Rightarrow {\left( 3 \right)^2} - {\left( 3 \right)^2} = {c^2}$
$\Rightarrow 36 - 9 = {c^2}$
Simplify the terms,
$\Rightarrow 27 = {c^2}$
Hence, in simplified way we get:
$\Rightarrow 3\sqrt 3 = c$
Now, let’s graph the solution:
We can set the center at $\left( {0,0} \right)$ .You might know that the vertices will be units away from the center in opposite directions. In our case, since the ellipse is vertical, they would be up and down the y-axis:
Vertices: $\left( {0,0 \pm 6} \right) = \left( {0,6} \right),\left( {0, - 6} \right)$
The co vertices are b units away, but in the different set of directions (in this case, to the left and right of the vertex):
Covertices: $\left( { \pm 3,0} \right) = \left( {3,0} \right),\left( { - 3,0} \right)$
The foci are on the same line, the major axis, but are c units away:
Foci: $\left( {0,0 \pm 3\sqrt 3 } \right) = \left( {0,3\sqrt 3 } \right),\left( {0, - 3\sqrt 3 } \right)$
We can plot these points on a graph and draw a smooth line through the vertices and co vertices. Hence the graph is represented as:

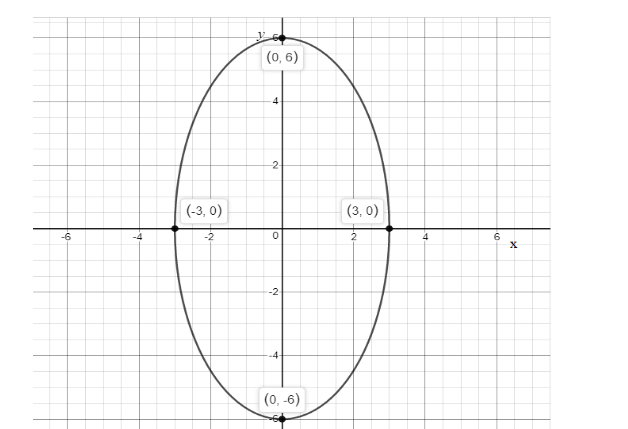
Note : To graph an Ellipse, we must know that an ellipse is the locus of all those points in a plane such that the sum of their distances from two fixed points in the plane, is constant. An ellipse is formed when a cone is intersected by a plane at an angle with respect to its base and it has two focal points and the sum of the two distances to the focal point, for all the points in the curve, is always constant.