Question

How do you graph the complex number $5-2i$ in the complex plane?

Answer 1

We find the similarities and the differences between the cartesian and complex plane. We try to express the complex number in the form of a real and complex line. Based on the values, we plot the point on the argand plane.

Complete step-by-step solution:
We have to plot the complex number $5-2i$ in the complex plane.
The representation of an arbitrary complex number is $z=x+iy$.
We take the $i$ as the complex identity. The values for $x,y\in \mathbb{R}$.
The complex plane is called the argand plane or the gauss plane. We take the two real constants and place those values in the coordinates form in the plane.
In case of cartesian coordinates we put the values for $\left( x,y \right)$ in the axes. We do the same thing for the complex plane but the axes are not both real axes.
Pulling the similarity with the cartesian coordinates, we will put the values of the real coefficients of $z=x+iy$.
The vertical axis of the complex plane will represent the coefficients associated with the complex $i$ and the horizontal axis of the complex plane will represent the coefficients associated with the real part. The unit values are identical to the cartesian plane.
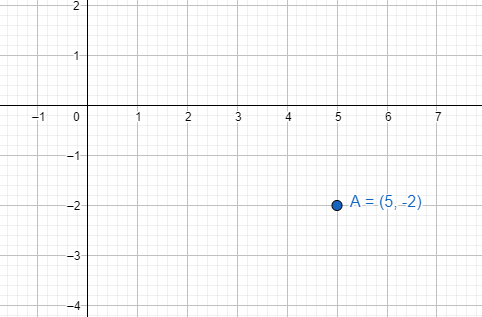
Now for $5-2i$, we will take 5 units along the positive side of the real axis and 2 units along the negative side of the complex axis.
The point in the graph looks identical to the point $\left( 5,-2 \right)$ in the cartesian plane.

Note: The complex plane consists of two number lines that intersect in a right angle at the point. Complex numbers can also be expressed in vector form or polar form.