Question

How do you graph $\tan \left( {\dfrac{x}{2}} \right) + 1$?

Answer 1

To graph the tangent function, we mark the angle along the horizontal x axis, and for each angle, we put the tangent of that angle on the vertical y-axis and the curve obtained is positive infinity in one direction and negative infinity in the other.

Complete step by step solution:
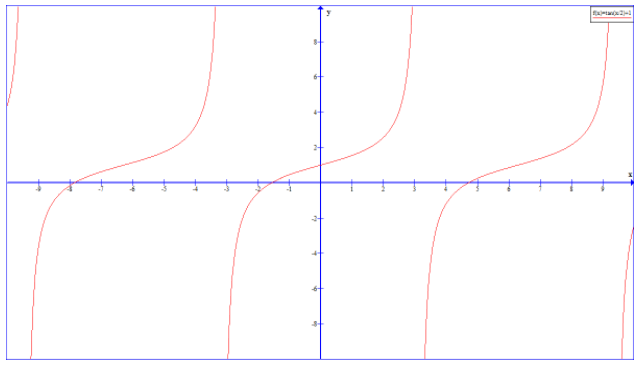
To graph the function $\tan \left( {\dfrac{x}{2}} \right) + 1$, as we know the shape of the tangent curve is the same for each full rotation of the angle and so the function is called 'periodic'.
And we must know a few points before sketching the graph.
The constant +1 in the function represents how much the graph is to be raised. We can find the period which are the lengths at which the function repeats itself, in which $\tan \left( x \right)$ has a period of $\pi$, so that $\tan \left( {\dfrac{x}{2}} \right)$ has a period of $2\pi$, since the angle is divided by 2 in the function given and$\tan \left( x \right)$ is undefined when $\cos \left( x \right) = 0$ and is zero when $\sin \left( x \right) = 0$ because
$\tan \left( x \right) = \dfrac{{\sin \left( x \right)}}{{\cos \left( x \right)}}$.
In the graph we can see that the function has vertical asymptotes at π intervals so the period is π and when $x = 0,y = 0$.
So, if you have $\tan x + 1$ it shifts all the y values up by one $\tan \left( {x2} \right)$is a vertical shift and it doubles the period to $2\pi$.

Note:
To sketch the trigonometry graphs of the functions – Sine, Cosine and Tangent, we need to know the period, phase, amplitude, maximum and minimum turning points. Hence based on this we can graph the derivative of a function. And the tangent function has a range that goes from positive infinity to negative infinity.