Question

How do you graph $r=\theta$ ?

Answer 1

We know that $\left( r,\theta \right)$ are polar coordinates, where r is the distance between the point and origin and $\theta$ is the angle between the line joining the origin and the point on X-axis. We will start substituting the value of $\theta$ from zero and increase gradually to find the desired answer.

Complete step by step solution:
We have given an expression $r=\theta$.
We have to plot a graph for the given equation.
Now, we know that $\left( r,\theta \right)$ are polar coordinates, where r is the distance between the point and origin and $\theta$ is the angle between the line joining the origin and the point on X-axis.
Now, we know that the value of $\theta$ starts from zero i.e. from origin and goes in the counter clockwise direction. The graph goes curved when the value of $\theta$ increases.
When the value of $\theta$ increases from $0\text{ to }\dfrac{\pi }{2}$ the graph goes in the counterclockwise direction and farther from the origin because the Cartesian coordinates will be
$\Rightarrow x=r\cos \theta$ and $y=r\sin \theta$
When $\theta =\dfrac{\pi }{2}$ we will get
$\Rightarrow x=r\cos \dfrac{\pi }{2}$ and $y=r\sin \dfrac{\pi }{2}$
$\Rightarrow x=\dfrac{\pi }{2}\times 0$ and $y=\dfrac{\pi }{2}\times 1$
$\Rightarrow x=0$ and $y=\dfrac{\pi }{2}$
So the graph intercepts the Y-axis at $\dfrac{\pi }{2}$.
Similarly when $\theta$ increases from to $\pi$ the graph intercepts X-axis at $\pi$.
We will get the graph as

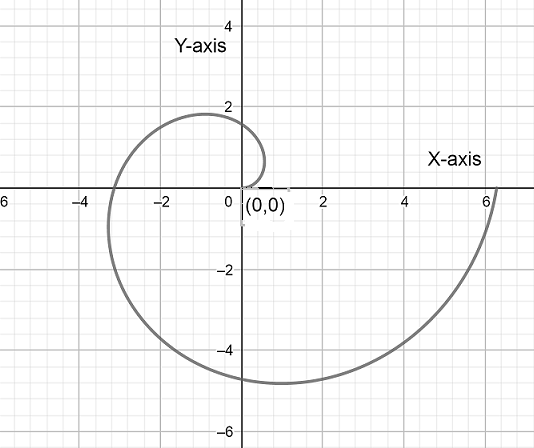
Hence above is the required graph of the given expression.

Note: To plot a graph first we need to find the values of Cartesian coordinates. Then by finding some values of points we will draw a graph. We need to write r and $\theta$ in terms of x and y to plot a graph in a Cartesian plane.