Solveeit Logo
Login

Question

Question: How do you graph \( r = 2\sin \theta \) ?...

How do you graph r=2sin⁡θr = 2\sin \theta ?

Explanation

Solution

Hint : The given equation is in the polar form of a conic section. To graph this equation on a cartesian plane we have to convert this equation into standard form or rectangular form. To convert this equation we can use the following conversions,
x=rcos⁡θ y=rsin⁡θ   x = r\cos \theta \\\ y = r\sin \theta \;
where θ\theta is the angle that the line joining origin and the general point makes with the x-axis and rr is the magnitude or the distance of the point from origin given as r2=x2+y2{r^2} = {x^2} + {y^2} .

Complete step by step solution:
We have been given to graph the equation r=2sin⁡θr = 2\sin \theta .
Since this equation includes the angle θ\theta and the magnitude rr , this is in the polar form. To graph this equation we will first convert it into standard form or rectangular form such that we get an equation in terms of xx and yy . We can use x=rcos⁡θ,    y=rsin⁡θ    and    r2=x2+y2x = r\cos \theta ,\;\;y = r\sin \theta \;\;and\;\;{r^2} = {x^2} + {y^2} .
From y=rsin⁡θy = r\sin \theta , we have sin⁡θ=yr\sin \theta = \dfrac{y}{r} .
From r2=x2+y2{r^2} = {x^2} + {y^2} , we have r=x2+y2r = \sqrt {{x^2} + {y^2}}
Thus the given equation becomes,
r=2sin⁡θ ⇒x2+y2=2yr=2yx2+y2 ⇒x2+y2=2y   r = 2\sin \theta \\\ \Rightarrow \sqrt {{x^2} + {y^2}} = 2\dfrac{y}{r} = \dfrac{{2y}}{{\sqrt {{x^2} + {y^2}} }} \\\ \Rightarrow {x^2} + {y^2} = 2y \;
We have the coefficient of x2{x^2} is equal to the coefficient of y2{y^2}. So this equation will represent a circle in the cartesian plane.
We can simplify the equation as,
x2+y2=2y ⇒x2+y2−2y=0 ⇒x2+y2−2y+1=1 ⇒x2+(y−1)2=12   {x^2} + {y^2} = 2y \\\ \Rightarrow {x^2} + {y^2} - 2y = 0 \\\ \Rightarrow {x^2} + {y^2} - 2y + 1 = 1 \\\ \Rightarrow {x^2} + {\left( {y - 1} \right)^2} = {1^2} \;
Thus the circle is centered at the point (0,1)\left( {0,1} \right) and the radius is 11 .
This can be drawn on the graph as follows,

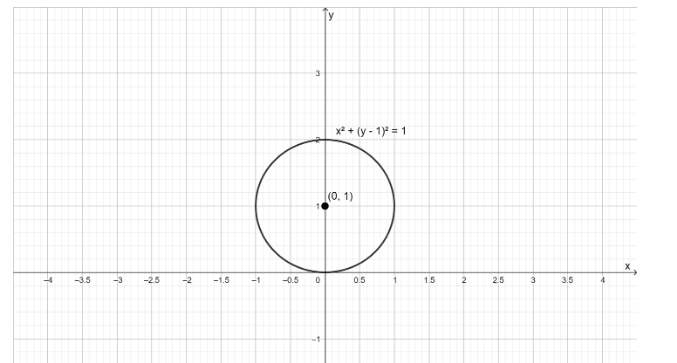
Hence, this is the graph of the given equation. Here rr is the distance of the general point on the curve from origin and θ\theta is the angle that the line joining the origin and the general point will make with the x-axis.

Note : We converted the given polar form of the equation into the rectangular form to graph the equation in a cartesian plane. The rectangular form is given in terms of xx and yy . After the conversion we have to determine what type of curve this equation represents or else we have to find the critical points using the derivatives.