Question

How do you graph ${r^2} = cos(2\theta )?$

Answer 1

In this question we have to find the graph given polar form. Next, we use some interval and then simplify to arrive at our final answer. Next we draw graphs in the given polar function complete step by step solution.The trigonometric functions (also called circular functions, angle functions or goniometric functions) are real functions which relate an angle of a right-angled triangle to ratios of two side lengths.
The polar form of a complex number is another way to represent a complex number. The form $z = a + bi$ is called the rectangular coordinate form of a complex number. The horizontal axis is the real axis and the vertical axis is the imaginary axis.

Complete step by step answer:
Given:
$\Rightarrow {r^2} = cos(2\theta )$
The problem with this particular equation is that
(a) it’s only defined for $\dfrac{{ - \pi }}{4} \leqslant \theta \leqslant \dfrac{\pi }{4}$ , so incrementing by $\dfrac{\pi }{2}$ will not get you many points, and (b) each value of $\theta$ yields two values of r, $r = \pm co{s^2}\theta$ , so if you forget one of the values, you lose out.
It’s not defined for $\theta < \dfrac{\pi }{4}$ because that would make and there’s No value of r that will have a negative square root.
Which means that incrementing by $\dfrac{\pi }{2}$ won’t give you much.
So what you need to do is recall that you know, from basic trig, the values of $cos\dfrac{\pi }{2} = 0$ , $cos\dfrac{\pi }{3} = \dfrac{1}{2}$ , $cos\dfrac{\pi }{4} = \dfrac{{\sqrt 2 }}{2}$ , $cos\dfrac{\pi }{6} = \dfrac{{\sqrt 3 }}{2}$ (and if you are really lucky, $cos\left( {\dfrac{\pi }{5} = \dfrac{\phi }{2}} \right)$ .
Thus, you can plot $r = \pm \sqrt {cos2\theta }$ for the 11points
$\theta = \dfrac{{ - \pi }}{6},\dfrac{{ - \pi }}{4},\dfrac{{ - \pi }}{8},\dfrac{{ - \pi }}{{10}},\dfrac{{ - \pi }}{{12}},0,\dfrac{\pi }{{12}},\dfrac{\pi }{{10}},\dfrac{\pi }{8},\dfrac{\pi }{6},\dfrac{\pi }{4}$ .
We called lemniscate, the graph looks like, symmetrical about the initial line $\theta = 0$ and the pole $r{\text{ }} = {\text{ }}0$ .

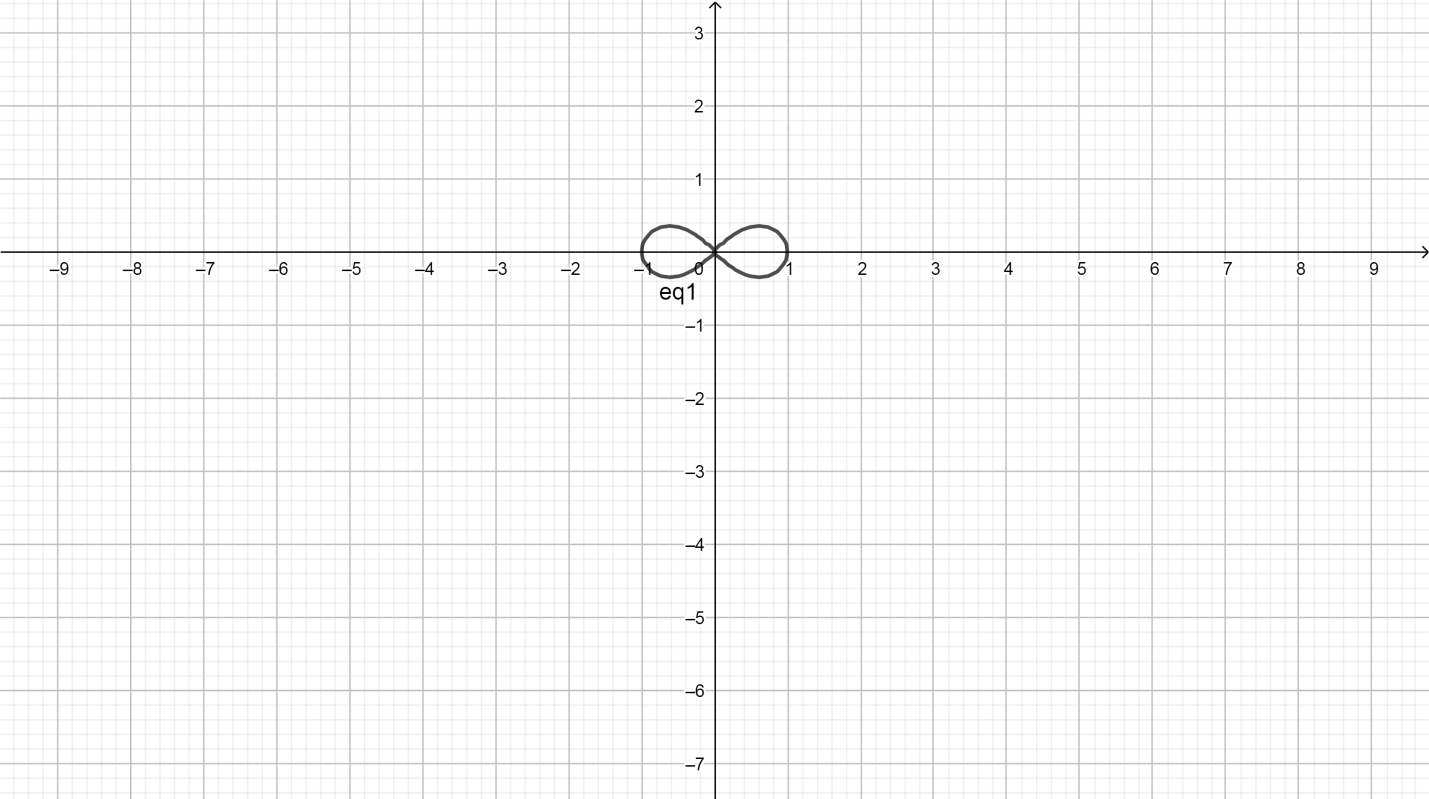
This is the required graph.

Note: We have to remainder that,
To get the area, you need to do an integral. Another answer suggested the integration formula $A = \int\limits_a^b {f\left( \theta \right)d\theta }$ , but that’s wrong because it’s based on rectangular coordinates, not polar coordinates.
The formula in rectangular coordinates is $\int {ydx}$ because $ydx$ is the area of an infinitesimal rectangle. However, in polar coordinates, the infinitesimal area isn’t a rectangle; it’s a triangle with an altitude of and a base of $rd\theta$ . The area of that infinitesimal triangle is $\dfrac{1}{2}{r^2}\theta$
So the general formula for the area in polar coordinates is $\int\limits_a^b {\dfrac{1}{2}{r^2}d\theta }$. In this case, you have a formula for ${r^2}$ , and you have to double the result because of the two possible values for r. So you’ll need to evaluate $2\int\limits_{\dfrac{{ - \pi }}{4}}^{\dfrac{\pi }{4}} {\dfrac{1}{2}\cos 2\theta d\theta }$ .
It’s relatively simple, but we watch out for all the factors of 2 and $\dfrac{1}{2}$ that get into the mess.