Question

How do you graph $r=2+4\sin \theta$ on graphing utility?

Answer 1

We recall polar coordinate sand polar curves. We first plot Cartesian curve $y=2+4\sin x$ and from there we find maximum, minimum values of $y$ corresponding to angles$n=\dfrac{n\pi }{2},n\in Z$. We take accordingly $\theta =\dfrac{n\pi }{2}$ and find $r$. We use the fact that the polar curves of the type $r=a\pm b\sin \theta ,a < b$ is a limacon with inner loop to draw the graph.

Complete step by step answer:
We know that in the polar coordinates $\left( r,\theta \right)$ is where $r$ is the radial distance from the origin and $\theta$ is the angle made by the line joining the point and the origin with the $x-$axis. The curve joined by points $\left( r,\theta \right)$ is called the polar curve.
We know $\sin \theta$ is a periodic function with period $2\pi$. The maximum value sine is $\sin \theta =1$ when $\theta =\left( 4n+1 \right)\dfrac{\pi }{2},n\in Z$ and the minimum value of sine is $\sin \theta =-1$ when $\theta =\left( 4n+3 \right)\dfrac{\pi }{2},n\in Z$. Let us first draw the graph $y=2+4\sin x$ as a Cartesian curve. Here $4\sin x$ will increase peaks of the sine curve by 4 times and then $2+4\sin x$ will shift the curve towards left by 2. We have the graph as

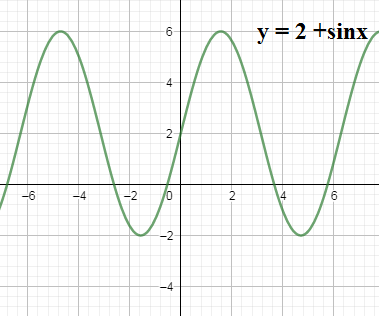
We know that the polar graph of $r=a\pm b\sin \theta ,a < b$ is a limacon with an inner loop. Let us observe the above plot we have when $\theta =0,y=2\Rightarrow r=2$ and when $\theta =n\pi \left( n\in Z \right)\Rightarrow r=2$since $\sin \left( n\pi \right)=0$.So we get two points $\left( 0,2 \right),\left( \pi ,2 \right)$on the $x-$ which represents axis with for the polar curve.
We see when $\theta =\left( 4n+1 \right)\dfrac{\pi }{2},n\in Z$ we get $r=6$ from the upper peaks and when $\theta =\left( 4n+3 \right)\dfrac{\pi }{2},n\in Z$ we get $r=-2$ from the lower peaks but since $r$ is a distance we have to take the modulus to have $r=\left| -2 \right|=2$. So we get the point the polar coordinates as $\left( \dfrac{\pi }{2},6 \right),\left( \dfrac{\pi }{2},2 \right)$. So the required limacon graph of the given function is

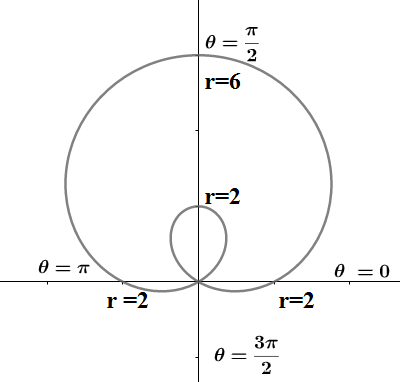
Note:
We note the polar graph of $r=a\pm a\sin \theta ,r=a\pm a\cos \theta$ are cardioids passing through origin . The polar graphs of $r=a\pm b\sin \theta \left( a < b \right),r=a\pm b\cos \theta \left( a < b \right)$ are limacons with an inner loop. The polar graphs of $r=a\pm b\sin \theta \left( a > b \right),r=a\pm b\cos \theta \left( a > b \right)$ are limacons without an inner loop. We note that limacon is a roulette formed by the path of a point fixed to a circle when that circle rolls around the outside of a circle of equal radius.