Solveeit Logo
Login

Question

Question: How do you graph \(r = 1 - \sin \left( \theta \right)\) ?...

How do you graph r=1−sin⁡(θ)r = 1 - \sin \left( \theta \right) ?

Explanation

Solution

The given expression is r=1−sin⁡(θ)r = 1 - \sin \left( \theta \right) which produces a cardioid. In the given expression r=1−sin⁡(θ)r = 1 - \sin \left( \theta \right) try to substitute different values for θ\theta and find the corresponding values of rr and plot the graph for the same values.

Complete step by step answer:
The given expression that is r=1−sin⁡(θ)r = 1 - \sin \left( \theta \right) which is a polar coordinate produces the cardioid. Cardioid is nothing but a curve or a graph that somewhat looks like a heart-shaped curve.
The graph of a cardioid looks as shown below.

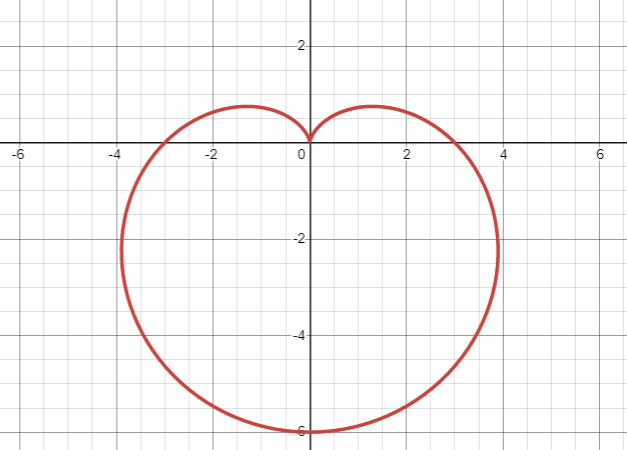
Now, to draw a graph for r=1−sin⁡(θ)r = 1 - \sin \left( \theta \right) , try to substitute different values for θ\theta which varies from 00 to 2π2\pi .
The below table gives us the values of sine function for different values:
\begin{array}{*{20}{c}} \theta &{{0^ \circ }}&{{{30}^ \circ }}&{{{45}^ \circ }}&{{{60}^ \circ }}&{{{90}^ \circ }}&{{{180}^ \circ }}&{{{270}^ \circ }}&{{{360}^ \circ }} \\\ {\sin \theta }&0&{\dfrac{1}{2}}&{\dfrac{{\sqrt 2 }}{2}}&{\dfrac{1}{2}}&1&0&{ - 1}&0 \end{array}
Now we consider different values for θ\theta to which we need to find the corresponding values of rr .
So let θ=0\theta = 0 now to find the corresponding value of rr we can write as below,
⇒r=1−sin⁡(0∘)=1−0=1\Rightarrow r = 1 - \sin \left( {{0^ \circ }} \right) = 1 - 0 = 1
At θ=30∘\theta = {30^ \circ } the value of rr is
⇒r=1−sin⁡(30∘)=1−12=12\Rightarrow r = 1 - \sin \left( {{{30}^ \circ }} \right) = 1 - \dfrac{1}{2} = \dfrac{1}{2}
At θ=60∘\theta = {60^ \circ } the value of rr is
⇒r=1−sin⁡(30∘)=1−12=12\Rightarrow r = 1 - \sin \left( {{{30}^ \circ }} \right) = 1 - \dfrac{1}{2} = \dfrac{1}{2}
At θ=90∘\theta = {90^ \circ } the value of rr we get as
⇒r=1−sin⁡(90∘)=1−1=0\Rightarrow r = 1 - \sin \left( {{{90}^ \circ }} \right) = 1 - 1 = 0
In the same way the values of rr can be listed as below for different values of θ\theta .

\theta &{{0^ \circ }}&{{{30}^ \circ }}&{{{60}^ \circ }}&{{{90}^ \circ }}&{{{180}^ \circ }}&{{{270}^ \circ }}&{{{360}^ \circ }} \\\ r&1&{\dfrac{1}{2}}&{\dfrac{1}{2}}&0&1&2&1 \end{array}$$ Now, plot the graph for the above values. Which is shown as in the below figure. ![](https://www.vedantu.com/question-sets/1a9bd857-cce5-4d94-b43d-8e8b6d6002936699755899161250136.png) **Therefore, the graph for the given expression $r = 1 - \sin \left( \theta \right)$ is as shown in the above figure.** **Note:** Whenever they ask us to draw a graph by giving an equation, then just take some values for one unknown that is for $\theta $ in the given equation and find the corresponding values of another unknown that is $r$ in this problem. Plot the same on a graph sheet as we did above.