Question

How do you graph $r=1-2\cos \theta$?

Answer 1

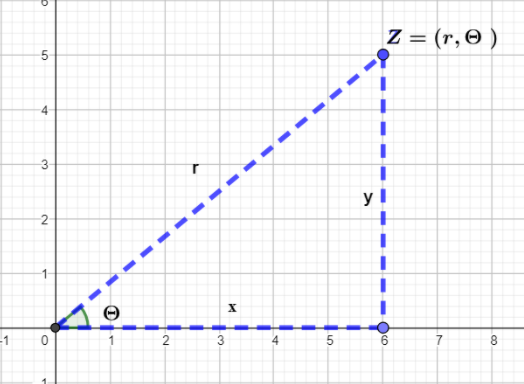
If the equation is of type $r=a-b\cos \theta$, then that equation is the polar equation. These equations will be graphed on the two-dimensional polar coordinate system. The point $Z=\left( r,\theta \right)$, where r is the distance from the origin and $\theta$ is the angle measured from the positive x-axis. It is measured counter-clockwise. We will find the value of r for some $\theta$ and try to plot it on the graph.

Complete step-by-step solution:
Here, we will use polar coordinates and a polar coordination system. So,
The point $Z=\left( r,\theta \right)$, where r is the distance from the origin and $\theta$ is the angle measured from the positive x-axis. It is measured counter-clockwise.

It is given in the question that $r=1-2\cos \theta$ and we have been asked to draw the graph of the given equation.
Now, we will find the value of r for different-different $\theta$.
$\Rightarrow r=1-2\cos \theta$
Now, we will put $\theta =0$ and label the point as A.
$\Rightarrow r=1-2\cos \left( 0 \right)$
And we know that $\cos \theta =\cos 0=1$
$\Rightarrow r=1-2\left( 1 \right)$
$\Rightarrow r=-1$
So we get A = (-1,0)
Now, we will put $\theta =\dfrac{\pi }{6}$ and label the point as B.
$\Rightarrow r=1-2\cos \left( \dfrac{\pi }{6} \right)$
And we know that $\cos \theta =\cos \left( \dfrac{\pi }{6} \right)=\dfrac{\sqrt{3}}{2}$
$\Rightarrow r=1-2\left( \dfrac{\sqrt{3}}{2} \right)$
$\Rightarrow r=1-1.73$
$\Rightarrow r=-0.73$
So we get, B = $\left( -0.73,\dfrac{\pi }{6} \right)$
Now, we will put $\theta =\dfrac{\pi }{4}$ and label the point as C.
$\Rightarrow r=1-2\cos \left( \dfrac{\pi }{4} \right)$
And we know that $\cos \theta =\cos \dfrac{\pi }{4}=\dfrac{1}{\sqrt{2}}$
$\Rightarrow r=1-2\left( \dfrac{1}{\sqrt{2}} \right)$
$\Rightarrow r=1-1.41$
$\Rightarrow r=-0.41$
So we get, C = $\left( -0.41,\dfrac{\pi }{4} \right)$
Now, we will put $\theta =\dfrac{\pi }{3}$ and label the point as D.
$\Rightarrow r=1-2\cos \left( \dfrac{\pi }{3} \right)$
$\Rightarrow r=1-2\left( \dfrac{1}{2} \right)$
$\Rightarrow r=1-1$
$\Rightarrow r=0$
So we get, D = $\left( 0,\dfrac{\pi }{3} \right)$
Now, we will put $\theta =\dfrac{\pi }{2}$ and label the point as E.
$\Rightarrow r=1-2\cos \left( \dfrac{\pi }{2} \right)$
And we know that $\cos \theta =\cos \dfrac{\pi }{2}=0$
$\Rightarrow r=1-2\left( 0 \right)$
$\Rightarrow r=1$
So we get, E = $\left( 1,\dfrac{\pi }{2} \right)$
Now, we will put $\theta =\dfrac{3\pi }{4}$ and label the point as G.
$\Rightarrow r=1-2\cos \left( \dfrac{3\pi }{4} \right)$
And we know that $\cos \theta =\cos \dfrac{3\pi }{4}=-\dfrac{1}{\sqrt{2}}$
$\Rightarrow r=1-2\left( -\dfrac{1}{\sqrt{2}} \right)$
$\Rightarrow r=1+1.41$
$\Rightarrow r=2.41$
So we get, G = $\left( 2.41,\dfrac{3\pi }{4} \right)$
Now, we will put $\theta =\pi$ and label the point as F.
$\Rightarrow r=1-2\cos \pi$
And we know that $\cos \theta =\cos \pi =-1$
$\Rightarrow r=1-2\left( -1 \right)$
$\Rightarrow r=1+2$
$\Rightarrow r=3$
So we get, F = $\left( 3,\pi \right)$
Now, we will plot all the points on the polar graph.
And then, we will join the points on the graph. Therefore, we get

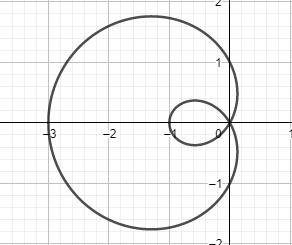
Hence, we have found the required graph.

Note: Whenever we get this type of problem, try to find the easiest points on the graph and locate them. Also, we do not want to do the calculation mistake as it leads to the wrong graph formation.