Question

How do you graph quadratic function $y={{x}^{2}}-4x+7$?

Answer 1

In the given question, we have been asked the steps for plotting a graph of a given quadratic equation. We will plot the graph of a given quadratic equation using vertex form. In order to graph a quadratic using vertex form, first we need to find the vertex of the given equation. Later we will find the y-intercept and the x-intercept and then plot the points we found in the above steps. In this way we can graph a quadratic equation using vertex form.

Complete step by step solution:
We have given that,
$y={{x}^{2}}-4x+7$
Converting into vertex form,
We have,
$y={{x}^{2}}-4x+7$
Using the vertex form of the equation; i.e.
$y=a{{\left( x-h \right)}^{2}}+k$
Where,
$a$ equals to the coefficient of ${{x}^{2}}$.
‘h’ is the x-coordinate of the vertex.
‘k’ is the y-coordinate of the vertex.
Vertex of the given equation $y={{x}^{2}}-4x+7$ is;
Now, solving for the value of ‘x’ and ‘y’,
$y={{x}^{2}}-4x+7$
Here ‘a’ is the coefficient of first term and b is the coefficient of ‘x’.
$\Rightarrow x=\dfrac{-b}{2a}=\dfrac{-\left( -4 \right)}{2}=2$
$\Rightarrow x=2$
Now, solving for the value of ‘y’.
Putting x = -7 in the given equation, we get
$\Rightarrow y={{\left( 2 \right)}^{2}}-4\left( 2 \right)+7$
Simplifying the above equation, we get
$\Rightarrow y=4-8+7=3$
$\Rightarrow y=3$
Therefore, the vertex$=(2,3)$.
Thus,
Vertex = (2, 3), ‘a’ = 1
Now, substituting these values in the vertex equation form, we obtain
$y=a{{\left( x-h \right)}^{2}}+k$
$y=1{{\left( x-\left( 2 \right) \right)}^{2}}+\left( 3 \right)$
Simplifying the above, we get
$y={{\left( x-2 \right)}^{2}}+3$
Hence, the equation $y={{x}^{2}}-4x+7$ in vertex form is$y={{\left( x-2 \right)}^{2}}+3$.
The equation of parabola is in the form ${{\left( x-a \right)}^{2}}=2p\left( y-b \right)$
Rewrite the equation in the form of parabola equation,
We have,
$y={{\left( x-2 \right)}^{2}}+3$
We can also write it as;
${{\left( x-2 \right)}^{2}}=\left( y-3 \right)$
Here 2p = 1, $p=\dfrac{1}{2}$
Thus,
The focus is $\left( 2,\dfrac{7}{2} \right)$
The vertex is (2, 3)
Now finding y-intercept
Put x = 0
$y={{x}^{2}}-4x+7={{0}^{2}}-4\left( 0 \right)+7=7$
Thus, we get the point i.e. (0, 7)
Plotting the points on the graph we found above,

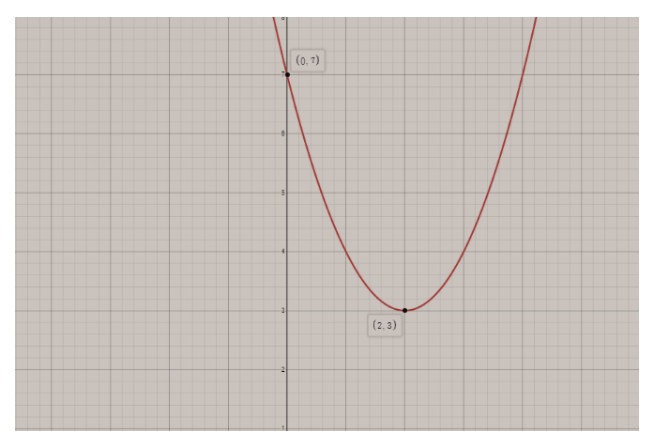
Therefore, this is the required graph of the $y={{x}^{2}}-4x+7$.

Note:
Students should be very well aware of the vertex form of the equation. Also, they should know about the concept of converting the given equation into vertex form. They should also be very careful while doing the calculations to avoid making errors. Students should also know to find the coordinates of the vertex.