Question

How do you graph $\left| z-i \right|=2$ in the complex plane?

Answer 1

We first assume the value of the complex number $z=x+iy$. We place the value in the equation $z-i$. Then we find the modulus value of $z-i$. We equate with 2 and then take the square of the equation. The equation becomes the form of a circle. We plot the equation in the graph.

Complete step-by-step solution:
We have to find the graph of $\left| z-i \right|=2$ in the complex plane.
Here $z$ works as a complex number. So, we assume the value as $z=x+iy$. Here $x$ and $y$ are real constants and $i$ works as the imaginary number.
The function of $\left| {} \right|$ is the representation of modulus value.
For general complex number $z=x+iy$, the modulus value will be $\left|z \right|=\sqrt{{{x}^{2}}+{{y}^{2}}}$.
Now we find the value of $z-i=\left( x+iy \right)-i=x+i\left( y-1 \right)$.
Now we find the modulus value of $z-i$.
$\left| x+i\left( y-1 \right) \right|=\sqrt{{{x}^{2}}+{{\left( y-1 \right)}^{2}}}$.
We have been given the equation $\left| z-i \right|=2$.
We place the values and get $\sqrt{{{x}^{2}}+{{\left( y-1 \right)}^{2}}}=2$.
We take the square on the both sides of the equation $\sqrt{{{x}^{2}}+{{\left( y-1 \right)}^{2}}}=2$ and value of the equation becomes ${{x}^{2}}+{{\left( y-1 \right)}^{2}}={{2}^{2}}=4$.
The equation is an equation of a circle.
We equalise ${{x}^{2}}+{{\left( y-1 \right)}^{2}}=4$ with the general equation of circle ${{\left( x-a \right)}^{2}}+{{\left( y-b \right)}^{2}}={{r}^{2}}$.
For the general equation we have the centre as $\left( a,b \right)$ and the radius as $r$.
Now we find the centre and the radius for ${{x}^{2}}+{{\left( y-1 \right)}^{2}}={{2}^{2}}$.
We have the centre as $\left( 0,1 \right)$ and the radius as 2.
Now we plot the equation in the graph.

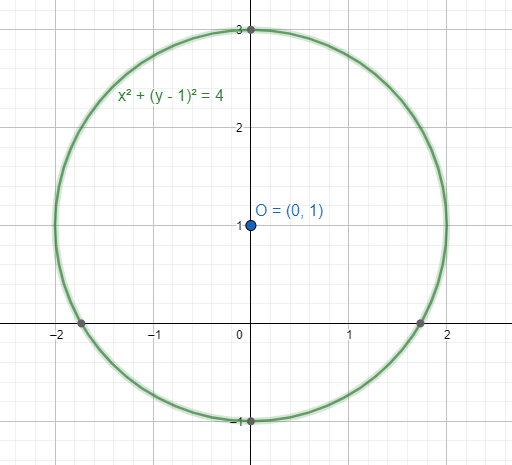
Note: We need to remember that in the complex plan the unit circle representation is always applicable for modulus values. The modulus value eliminates the imaginary part of the equation.