Question

How‌ ‌do‌ ‌you‌ ‌graph‌ ‌${{\left(‌ ‌x+4‌ ‌\right)}^{2}}+{{\left(‌ ‌y-1‌ ‌\right)}^{2}}=9$‌ ‌?‌

Answer 1

For answering this question we need to draw the graph related to the given expression${{\left( x+4 \right)}^{2}}+{{\left( y-1 \right)}^{2}}=9$ . If we observe carefully it is similar to the general form of circle given as ${{\left( x-{{x}_{1}} \right)}^{2}}+{{\left( y-{{y}_{1}} \right)}^{2}}={{r}^{2}}$ where $r$ is radius and $\left( {{x}_{1}},{{y}_{1}} \right)$ is the centre of the circle.

Complete step by step solution:
Now considering from the question we have been asked to draw the graph of the given expression ${{\left( x+4 \right)}^{2}}+{{\left( y-1 \right)}^{2}}=9$ .
From the basics of concept we know that the general form of the circle is given as ${{\left( x-{{x}_{1}} \right)}^{2}}+{{\left( y-{{y}_{1}} \right)}^{2}}={{r}^{2}}$ where $r$ is radius and $\left( {{x}_{1}},{{y}_{1}} \right)$ is the centre of the circle.
If we observe carefully the given expression is similar to the general form of the circle. And in the place of ${{r}^{2}}$ we have $9$ similarly in the place of $\left( {{x}_{1}},{{y}_{1}} \right)$ we have $\left( -4,1 \right)$ . Hence we can say that here the centre of the given circle is $\left( -4,1 \right)$ and radius is $3$ .

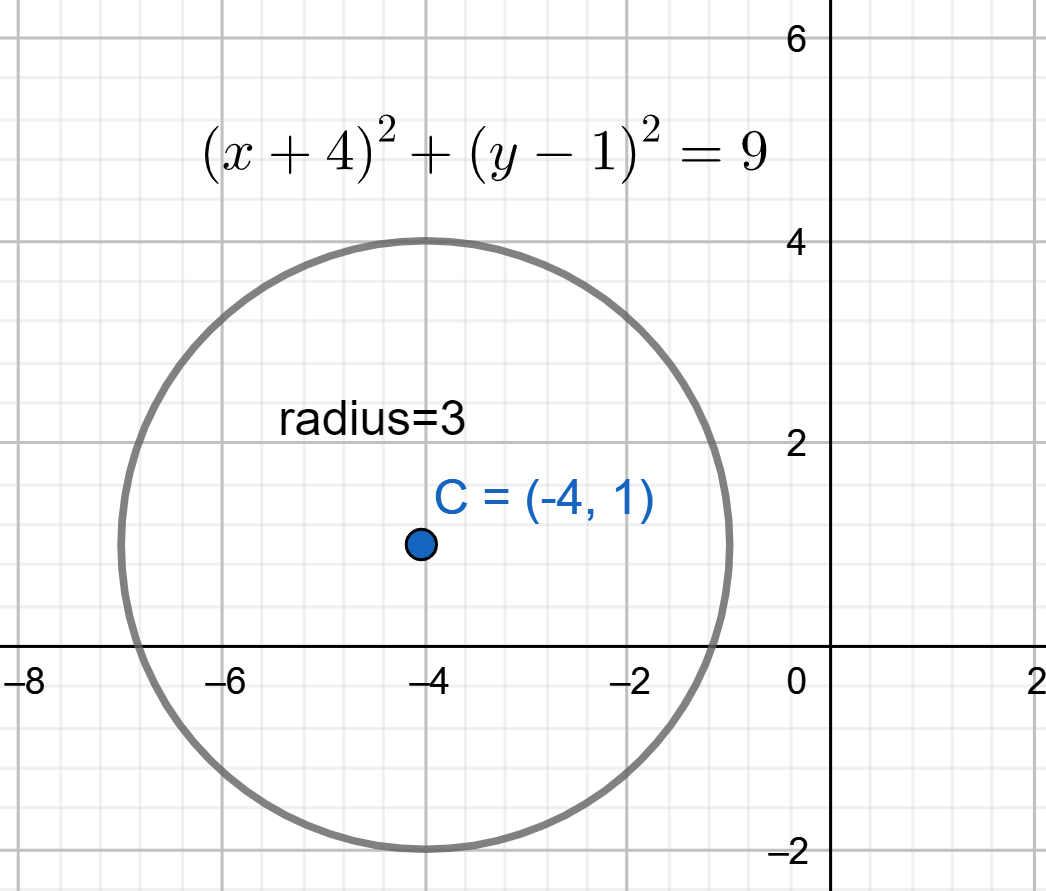
Hence let us plot the graph for a circle. Let us mark the centre and draw a circle with the required radius.
Therefore we can conclude that the graph of the given expression looks like the above one

Note: While answering questions of this type be sure with our concept that we apply during the process in between. This is a very simple and easy question. It does not involve much calculation. Similarly we have another expression for circle ${{x}^{2}}+{{y}^{2}}+2gx+2fy+c=0$ where radius is $\sqrt{{{g}^{2}}+{{f}^{2}}-c}$ and centre is $\left( -g,-f \right)$ .