Question

How do you graph ${{\left( x-3 \right)}^{2}}+{{\left( y+4 \right)}^{2}}=25$ ?

Answer 1

These types of problems are pretty straight forward and are very easy to solve. For such questions, we first need to analyse the given equation and by logic need to understand what the given equation represents. That whether the given equation represents a pair of straight lines or a circle or a parabola or an ellipse or a hyperbola.

Complete step-by-step solution:
The general equation for a conic is given by,
$a{{x}^{2}}+b{{y}^{2}}+2hxy+2gx+2fy+c=0$ . Now, this equation represents a circle if and only if the value of $a$ is equal to $b$ and $\sqrt{{{g}^{2}}+{{f}^{2}}-c}$ is greater than or equal to zero. For equal to zero the conic represents a point circle. We now need to compare our given equation with the general equation to evaluate our findings.
We now start off with our solution as,
From the given equation to our problem, we can clearly observe that the coefficient of $x$ is equal to the coefficient of $y$, and the value of $\sqrt{{{g}^{2}}+{{f}^{2}}-c}$ is greater than zero. Hence the given equation of the problem, represents a conic which is a circle. However the general equation of a circle is also represented as ${{x}^{2}}+{{y}^{2}}={{c}^{2}}$ , in which the centre of the circle is $\left( 0,0 \right)$ and the radius is $c$ . Now comparing our given equation, with that of the general equation we get the centre of the circle as $\left( 3,-4 \right)$ and the radius as $5$ . Now, plotting the graph with these required information, we get,

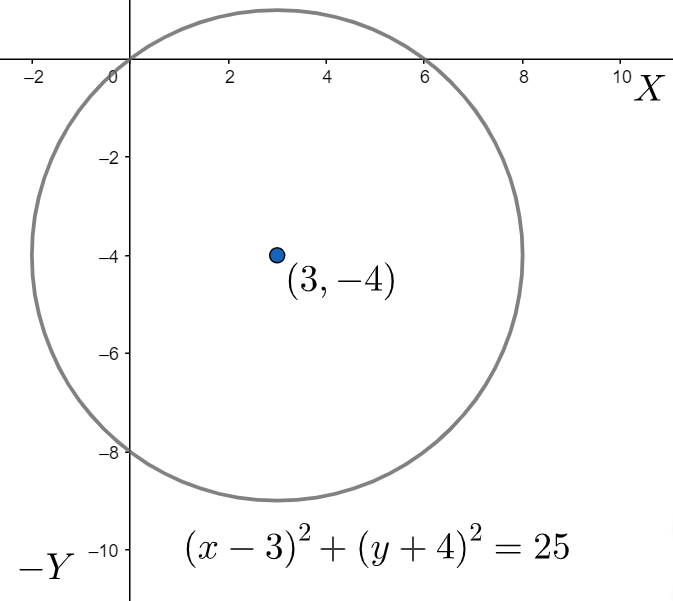
Note: For such kinds of problems, we need to keep in mind the general equation of conics and the various relations for various types of conic sections. In such problems we compare the given equation with that of the general one and then find out our required things to plot the graph. After plotting we mark the points of importance and write down what conic the equation represents.