Solveeit Logo
Login

Question

Question: How do you graph \[{\left( {x + 3} \right)^2} + \left( {{{\left( {y + 5} \right)}^2}} \right) = 16\]...

How do you graph (x+3)2+((y+5)2)=16{\left( {x + 3} \right)^2} + \left( {{{\left( {y + 5} \right)}^2}} \right) = 16?

Explanation

Solution

Here in this question, we have to plot a graph for the given equation. The given equation resembles or recognised as the standard equation for a circle, which is (x−h)2+(y−k)2=r2{\left( {x - h} \right)^2} + {\left( {y - k} \right)^2} = {r^2}, where (h,k)\left( {h,k} \right) is the centre of the circle and rr is the radius. For using these data, we can plot a required graph.

Complete step by step answer:
Equation of a Circle When the Centre is Origin: Consider an arbitrary point P(x,y)P\left( {x,y} \right) on the circle. Let ‘aa’ be the radius of the circle and origin (0,0)\left( {0,0} \right)can be found using the distance formula which is equal to- x2+y2=r2{x^2} + {y^2} = {r^2}
Equation of a Circle When the Centre is not an Origin: Let C(h,k)C\left( {h,k} \right) be the centre of the circle and P(x,y)P\left( {x,y} \right) be any point on the circle, the radius of a circle is ‘aa’.
the equation of the circle with centre (h,k)\left( {h,k} \right) and the radius ‘aa’ is:
(x−h)2+(y−k)2=a2{\left( {x - h} \right)^2} + {\left( {y - k} \right)^2} = {a^2}
which is called the standard form for the equation of a circle.
Consider, the given graph
⇒ (x+3)2+(y+5)2=16\Rightarrow \,{\left( {x + 3} \right)^2} + {\left( {y + 5} \right)^2} = 16
As we know, 16 is the square number of 4.
⇒ (x+3)2+(y+5)2=42\Rightarrow \,{\left( {x + 3} \right)^2} + {\left( {y + 5} \right)^2} = {4^2}
Which, resembles like a equation of the circle when the centre is not a origin i.e., (x−h)2+(y−k)2=a2{\left( {x - h} \right)^2} + {\left( {y - k} \right)^2} = {a^2}
Where, h=−3h = - 3, k=−5k = - 5 and a=4a = 4.
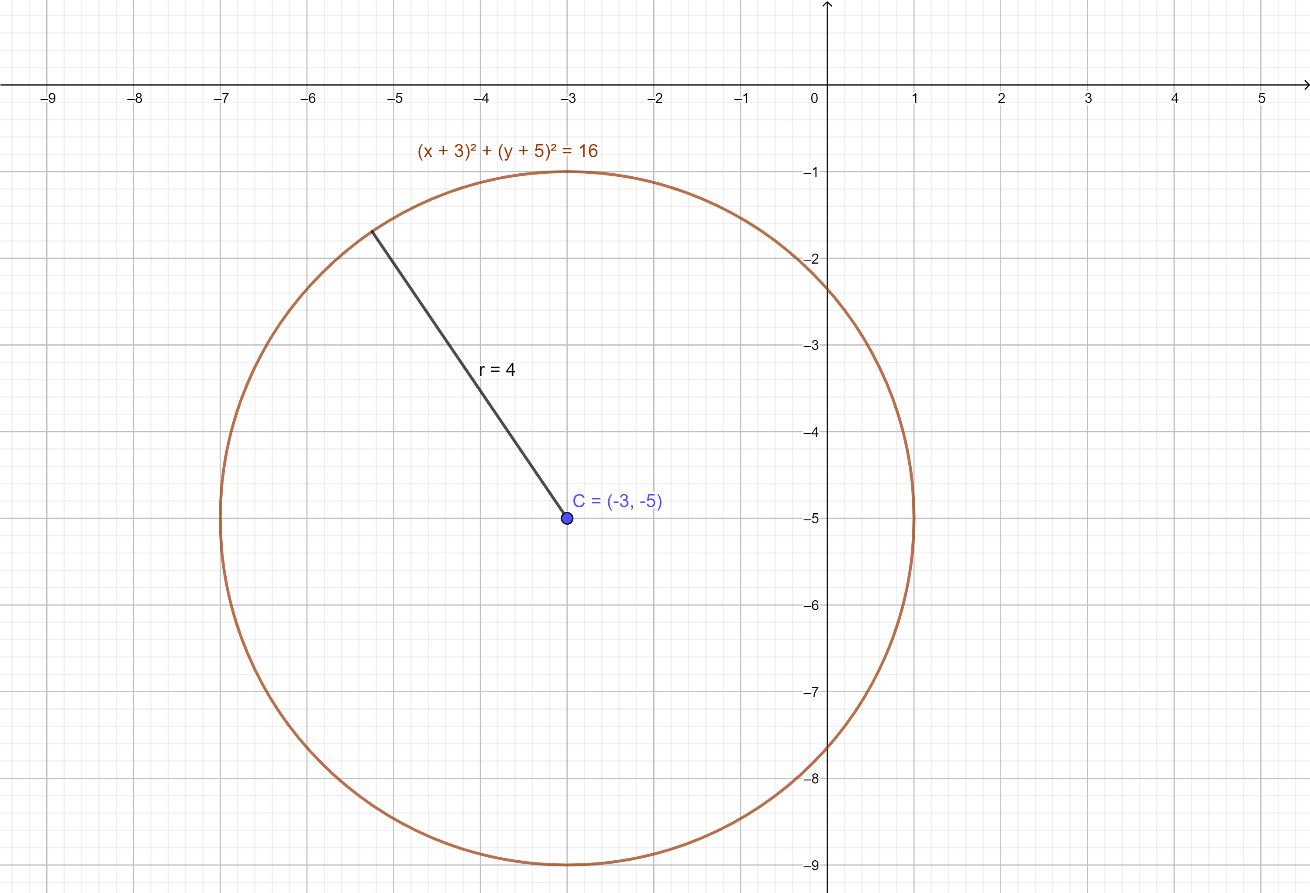
Centre of the circle is: C(−3,−5)C\left( { - 3, - 5} \right)
Radius of the circle: r=4r = 4
Hence, the graph of the equation (x−h)2+(y−k)2=r2{\left( {x - h} \right)^2} + {\left( {y - k} \right)^2} = {r^2} is given below:

Note: A circle is formed when an arc is drawn from the fixed point called the centre, in which all the points on the curve are having the same distance from the centre point of the centre. We know that there is a question that arises in case of circle whether being a function or not. It is clear that a circle is not a function.