Solveeit Logo
Login

Question

Question: How do you graph \({{\left( x+1 \right)}^{2}}+{{\left( y+2 \right)}^{2}}=9\)?...

How do you graph (x+1)2+(y+2)2=9{{\left( x+1 \right)}^{2}}+{{\left( y+2 \right)}^{2}}=9?

Explanation

Solution

In this question we have an expression which we will convert into the form of the equation of a circle. The general equation of a circle is (x−h)2+(y−k)2=r2{{\left( x-h \right)}^{2}}+{{\left( y-k \right)}^{2}}={{r}^{2}}, where (h,k)\left( h,k \right) is the center of the circle and rr is the radius of the circle. We will simplify the equation to get it in this form, and then compare it with the general form to get the values of h,kh,k and rr, and then plot then draw the circle on the graph.

Complete step by step solution:
We have the expression given to us as:
⇒(x+1)2+(y+2)2=9\Rightarrow {{\left( x+1 \right)}^{2}}+{{\left( y+2 \right)}^{2}}=9
Now we can write the terms in addition in the form of subtraction of a negative term as:
⇒(x−(1))2+(y−(−2))2=9\Rightarrow {{\left( x-\left( 1 \right) \right)}^{2}}+{{\left( y-\left( -2 \right) \right)}^{2}}=9
Now the term 99 in the right-hand side can be written as the square of the term 33 as:
⇒(x−(1))2+(y−(−2))2=32\Rightarrow {{\left( x-\left( 1 \right) \right)}^{2}}+{{\left( y-\left( -2 \right) \right)}^{2}}={{3}^{2}}
Now we can see that the above expression is in the form of the general equation of a circle which is (x−h)2+(y−k)2=r2{{\left( x-h \right)}^{2}}+{{\left( y-k \right)}^{2}}={{r}^{2}}.
On comparing the terms, we get the values of h,kh,k and rr as:
h=−1h=-1
k=−2k=-2
r=3r=3
Now the center of the circle is the point (h,k)\left( h,k \right).therefore, we get the radius of the circle as:
(−1,−2)\left( -1,-2 \right).
Now on plotting this point on the graph, we get:

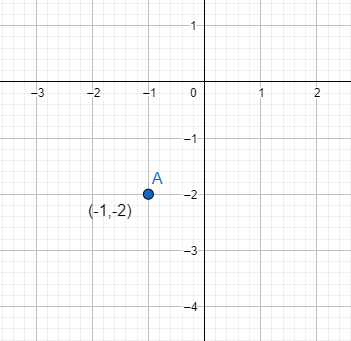
Now the radius of the circle is given by rr, therefore from the expression, we have r=3r=3.
Therefore, we will make a circle around point AA with the radius 33 as:

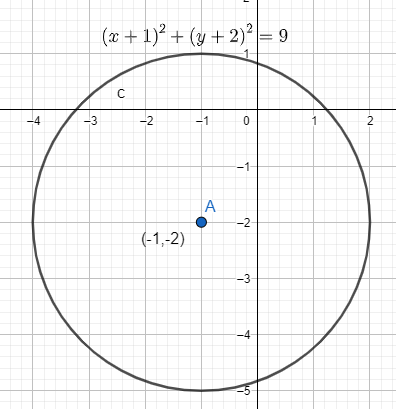
Which is the required solution.

Note: In this question when we took the square root of the term 99, we only considered the positive value of 33 and not the negative value since the radius is distance and distance cannot be negative.
The equation of a circle with its center at the origin can be written as x2+y2=r2{{x}^{2}}+{{y}^{2}}={{r}^{2}}, where rr is the radius of the circle.