Question

How do you graph $F(x,y) = \sqrt {{x^2} + {y^2} - 1} + \ln (4 - {x^2} - {y^2})$ ?

Answer 1

Hint : In the above given equation $F(x,y) = \sqrt {{x^2} + {y^2} - 1} + \ln (4 - {x^2} - {y^2})$ we will observe two independent variables $x$ and $y$ . Now we will replace these variables $x$ and $y$ as $r$ so $F(x,y) = f(r)$ m also denoted as $z$ .In order to plot the graph we need to convert the equation in polar form. Later on we will sketch a two dimensional graph for $z = \sqrt {{r^2} - 1} + \ln (4 - {r^2})$ and finally we will rotate it about $z$ axis.

Complete step-by-step answer :
As we know that in the above problem for which we need to sketch the graph consists of the given function which we have is
$F(x,y) = \sqrt {{x^2} + {y^2} - 1} + \ln (4 - {x^2} - {y^2})$
Here we will observe that $F$ is the given function of the independent variables $x$ and $y$ .
Now we will let $\sum {}$ be the surface of the given function $F$
Here it the $F(x,y) = f(r)$ in which
$r = \sqrt {{x^2} + {y^2}}$
Precisely we will observe that
$f(r) = \sqrt {{r^2} - 1} + \ln (4 - {r^2})$
Or $z = \sqrt {{r^2} - 1} + \ln (4 - {r^2})$

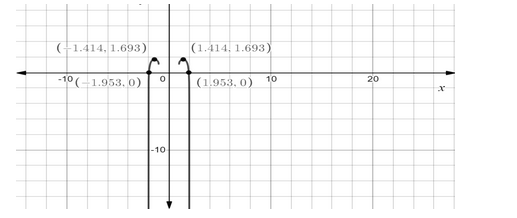
Now if we will revolve the graph around the $z$ axis we will get the graph of the given function as a surface of revolution. Hence the graph of the given function is sketched

Note : By substituting the values and equating it keeping the equation balanced we can draw the graph for the given equation.
Notes: The graph which is obtained in the above equation is the 3-Dimensional graph as it shows involvement of three variables $x,y{\text{ }}and{\text{ }}z$ . It is difficult to obtain these kinds of 3-Dimensional graphs through simple derivatives and coordinate concepts .To draw this graph knowledge of advanced mathematics concepts like solids of revolution is required.