Question

How do you graph $f(x) = {x^3} - 2x - 4$?

Answer 1

According to the question we have to determine the graph of the given expression $f(x) = {x^3} - 2x - 4$ which is as mentioned in the question. So, first of all to determine the required graph of the given polynomial expression we have to determine the y-intercept which can be obtained by substituting the value of the variable x as 0.
Now, we have to determine the x-intercept which can be determined by substituting the value of the variable y as 0.
Now, I have to determine the y-intercept which can be obtained by substituting the value of the variable x as -1, -2, -3.
Now, I have to determine the y-intercept which can be obtained by substituting the value of the variable x as 1, 2, 3.
Now, with the help of all points or we can say the y and x-intercepts we can draw the graph for the given expression and with the help of the table obtained.

Complete step-by-step solution:
Step 1: First of all to determine the required graph of the given polynomial expression we have to determine the y-intercept which can be obtained by substituting the value of the variable x as 0. Hence,
$\Rightarrow y = {0^3} - 2(0) - 4 \\\ \Rightarrow y = - 4$
Step 2: Now, we have to determine the x-intercept which can be determined by substituting the value of the variable y as 0. Hence,
$\Rightarrow 0 = {x^3} - 2x - 4 \\\ \Rightarrow {x^3} - 2x = 4$
We can not factor the cubic function above,
Step 3: Now, I have to determine the y-intercept which can be obtained by substituting the value of the variable x as -1, -2, -3. Hence,
On substituting $x = - 1$
$\Rightarrow y = {( - 1)^3} - 2( - 1) - 4 \\\ \Rightarrow y = - 1 + 2 - 4 \\\ \Rightarrow y = - 3$
Hence, the points obtained are $( - 1, - 3)$
On substituting $x = - 2$
$\Rightarrow y = {( - 2)^3} - 2( - 2) - 4 \\\ \Rightarrow y = - 8 + 4 - 4 \\\ \Rightarrow y = - 8$
Hence, the points obtained are $( - 2, - 8)$
On substituting $x = - 3$
$\Rightarrow y = {( - 3)^3} - 2( - 3) - 4 \\\ \Rightarrow y = - 27 + 6 - 4 \\\ \Rightarrow y = - 25$
Hence, the points obtained are $( - 3, - 25)$
Step 4: Now, I have to determine the y-intercept which can be obtained by substituting the value of the variable x as 1, 2, 3. Hence,
On substituting $x = 1$
$\Rightarrow y = {(1)^3} - 2(1) - 4 \\\ \Rightarrow y = 1 - 2 - 4 \\\ \Rightarrow y = - 5$
Hence, the points obtained are $(1, - 5)$
On substituting $x = 2$
$\Rightarrow y = {(2)^3} - 2(2) - 4 \\\ \Rightarrow y = 8 - 4 - 4 \\\ \Rightarrow y = 0$
Hence, the points obtained are $(2,0)$
On substituting $x = 3$
$\Rightarrow y = {(3)^3} - 2(3) - 4 \\\ \Rightarrow y = 27 - 6 - 4 \\\ \Rightarrow y = 17$
Hence, the points obtained are $(3,17)$
Step 5: Now, with the help of all points or we can say the y and x-intercepts we can draw the graph for the given expression and with the help of the table obtained.

x	y
-3	-25
-2	-8
-1	-3
0	-4
1	-5
2	0
3	17

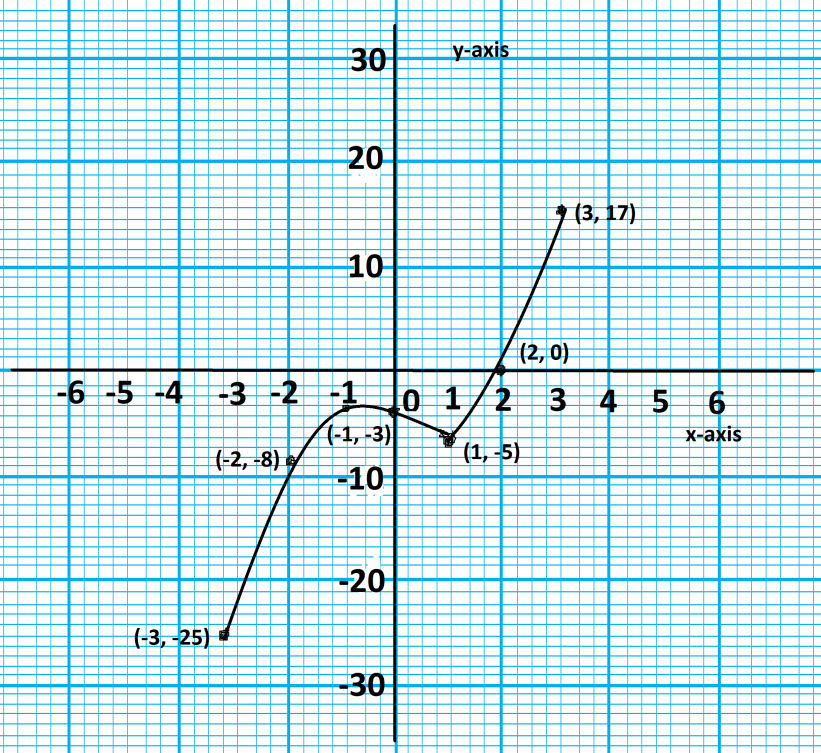
Hence, we have determined the graph for the given polynomial $f(x) = {x^3} - 2x - 4$ which is as mentioned below:

Note: To plot the points such as (a, b) in the graph it is necessary that first of all we have to plot point a in the x-axis of the quadrant then we have to plot point b to the y-axis of the graph.
On substituting the value of the variable y as 0 to obtain the x-intercept we can’t determine the required intercept due to the expression ${x^3} - 2x = 4$.