Question

How do you graph $f(x)=\dfrac{2}{{{x}^{2}}-4x+4}$ using holes, vertical and horizontal asymptotes, x and y intercepts?

Answer 1

To find the holes check at which values of x, the function is undefined. To find the vertical asymptote equate the denominator to zero. To find the horizontal asymptote compare the degree of the numerator and the degree of the denominator. To find the x and y intercepts, substitute $f(x)=0$ and $x=0$ respectively.

Complete step by step solution:
Holes in the graph of a rational function are the points on the curve of the function where the value of the function is not defined.
In a rational function, the value of the function f(x) is undefined when either both the numerator and the denominator are zero or both of them tend to infinity.
The given function is $f(x)=\dfrac{2}{{{x}^{2}}-4x+4}$.
Here, we can write ${{x}^{2}}-4x+4=(x-2)(x-2)$
With this, we can write the function as $f(x)=\dfrac{2}{(x-2)(x-2)}$ … (i)
In the equation (i), we can see that the value of the numerator is 2, which is non zero. This means that the number is defined at every point.
Therefore, there are no holes in the graph.
Vertical asymptote is the line that becomes a vertical tangent to the curve at infinite value of f(x). We can find the equation of the vertical asymptotes by equating the denominator to zero.
Therefore, equate the denominator to zero.
$\Rightarrow (x-2)(x-2)=0$
$\Rightarrow x=2$
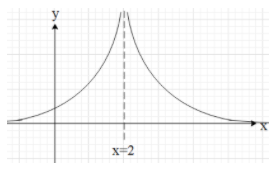
This means that the vertical asymptote for the graph is $x=2$.
Horizontal asymptote is tangent to the curve at infinite value of x. When the degree of the denominator is greater than the degree of the numerator, the horizontal asymptote is y-axis, i.e. $y=0$
In this case, the degree of the numerator is 0 and the degree of the denominator is 2. This means that the degree of the denominator is greater than the degree of the numerator. Therefore, the horizontal asymptote is $y=0$.
x intercepts are the points where the curve cuts or touches the x axis. We can find these points by equating the function f(x) to zero. However, the numerator is 2, which means that the function is never equal to zero.
y intercepts are points where the curve cuts or touches the y axis. We can find these points by substituting $x=0$ in the function.
Substitute $x=0$ in (i).
$\Rightarrow f(x)=y=\dfrac{2}{(0-2)(0-2)}$
$\Rightarrow y=\dfrac{2}{4}=\dfrac{1}{2}$
Therefore, the y intercept is $y=\dfrac{1}{2}$.
If we merge all this information, then the graph of the function will look like:

Note:
Note that the graph of a given function will never cross its vertical asymptote but the curve may cross its horizontal asymptote.
If the degree of the denominator is less than the degree of the numerator, then the graph of the rational function will have a slant asymptote.