Question

How do you graph $f(x) = 1 - \cos 3x$?

Answer 1

This problem deals with finding the graph of the given function. The function involves a trigonometric function which is a cosine trigonometric function. The general equation or a general function of a cosine function is denoted by $A\cos \left( {B\left( {x - C} \right)} \right) + D$. Where this particular function has a period, amplitude and phase shift. The period of a periodic function is the interval between two matching points on the graph. The period of cosine function is $2\pi$.

Complete step-by-step answer:
Any function is denoted in such a way, where $f(x) = A\cos \left( {B\left( {x - C} \right)} \right) + D$
$\Rightarrow f(x) = A\cos \left( {B\left( {x - C} \right)} \right) + D$
Here $A$ is the amplitude of the function, $P$ is the period of the function, $C$ is the phase shift and $D$ is the vertical shift of the given function.
$\Rightarrow P = \dfrac{{2\pi }}{B}$
Here on comparing the given function $f(x) = 1 - \cos 3x$ with the standard form of cosine function which is $f(x) = A\cos \left( {B\left( {x - C} \right)} \right) + D$
$\Rightarrow f(x) = 1 - \cos 3x$
Here there are two things to be observed which are the amplitude of the function is -1 and the vertical shift is 1. As the amplitude is negative, the graph will be on the side of the negative vertical axis.
Here the period is by $P = \dfrac{{2\pi }}{B}$, as given below, here $B$ is 3.
$\Rightarrow P = \dfrac{{2\pi }}{3}$
There is no phase shift. So the graph of $f(x) = 1 - \cos 3x$, is given below:

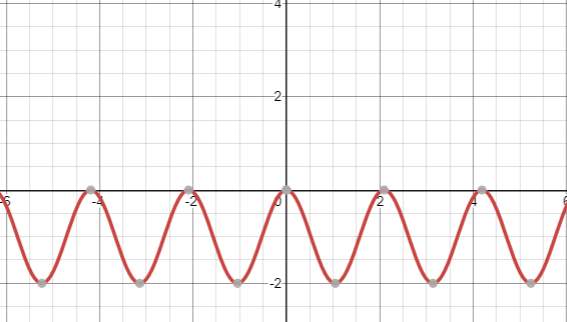
Final Answer: The amplitude, period, phase shift and vertical shift for $f(x) = 1 - \cos 3x$ are -1, $\dfrac{{2\pi }}{3}$ , 0 and 1 respectively.

Note:
Please note that the fundamental period of a function is the period of the function which are of the form, $f\left( {x + k} \right) = f\left( x \right)$ and $f\left( x \right) = f\left( {x + k} \right)$, then $k$ is called the period of the function and the function $f$ is called a periodic function. In other words, it is the distance along the x-axis that the function has to travel before it starts to repeat its pattern. The basic sine and cosine functions have a period of $2\pi$, while tangent has a period of $\pi$.