Question

How do you graph $f\left( x \right)=-{{x}^{2}}+2x+5$ and identify its x intercepts and vertex ?

Answer 1

The equation of in the question is a quadratic equation, so the graph of the equation is a parabola. The x intercepts are also the roots of the equation we can find the roots by quadratic formula. The x coordinate of vertex of the parabola is the mean of x coordinates of roots.

Complete step by step answer:
The given equation is $f\left( x \right)=-{{x}^{2}}+2x+5$
Let’s find the x intercepts or roots of the quadratic equation by using quadratic formula $\dfrac{-b\pm \sqrt{{{b}^{2}}-4ac}}{2a}$ where a is coefficient of ${{x}^{2}}$ , b is the coefficient of x and c is the constant term in a quadratic equation.
So the value of a in $f\left( x \right)=-{{x}^{2}}+2x+5$ is equal to -1, b is 2 and c is 5
The roots of the equation $\dfrac{-2\pm \sqrt{{{2}^{2}}-4\times -1\times 5}}{2\times -1}$
Further solving we get the roots are $1+\sqrt{6}$ and $1-\sqrt{6}$
We know that the x coordinate of vertex of the parabola is mean of x coordinates of roots
So the value of x coordinate of vertex is equal to $\dfrac{1+\sqrt{6}+1-\sqrt{6}}{2}=1$
So y coordinate of vertex is $f\left( 1 \right)=6$
The coefficient of ${{x}^{2}}$ in $f\left( x \right)=-{{x}^{2}}+2x+5$ in negative so the graph of $f\left( x \right)=-{{x}^{2}}+2x+5$ is a downward parabola with vertex (1,6) and passing through $\left( 1+\sqrt{6},0 \right)$ , $\left( 1-\sqrt{6},0 \right)$

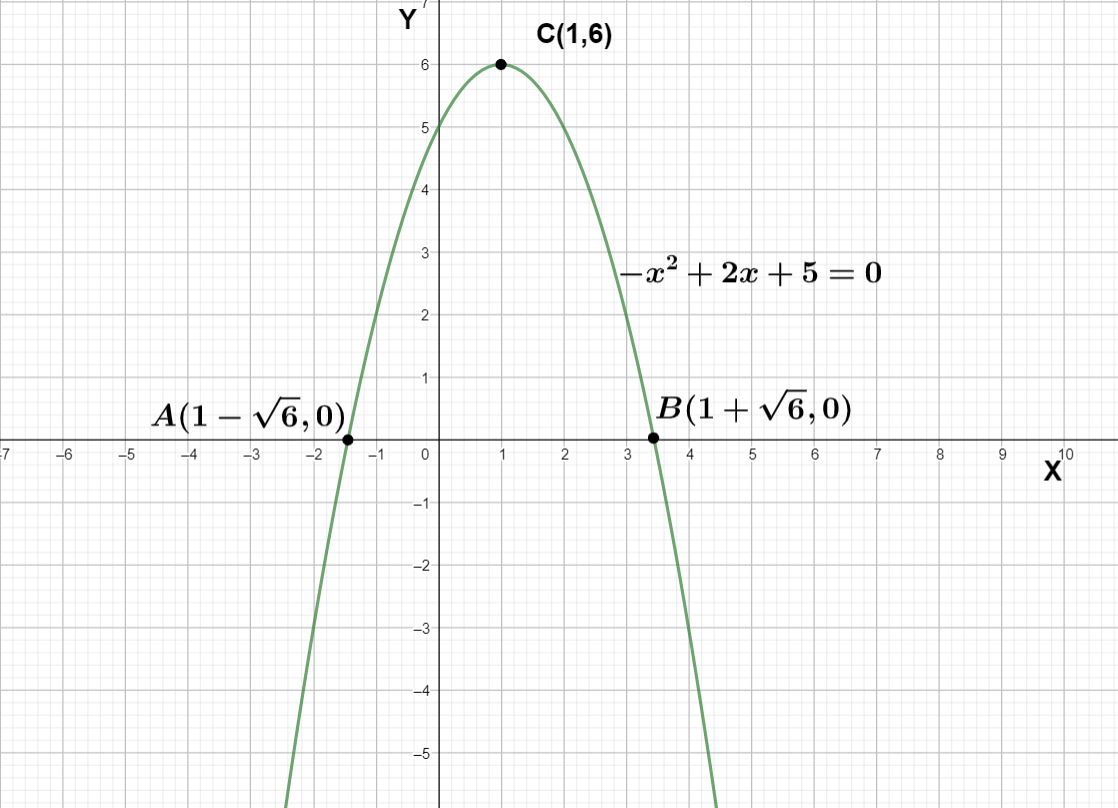
We can see the x intercepts are $1+\sqrt{6}$ and $1-\sqrt{6}$ and the vertex is point C (1,6)

Note:
Always remember that the upward or downward property of a parabola depends on the coefficient of ${{x}^{2}}$ in the quadratic equation. If the coefficient of ${{x}^{2}}$ is negative then the graph will be downward and if the coefficient is positive then the graph will be upward.