Question

How do you graph $F\left( x \right)={{\log }_{\dfrac{1}{3}}}\left( x+5 \right)$ ?

Answer 1

To graph $F\left( x \right)={{\log }_{\dfrac{1}{3}}}\left( x+5 \right)$ , we have to equate the RHS of this function to y. Then, we have to find the x and y intercepts by substituting $y=0$ and $x=0$ respectively. Then, we have to find the vertical asymptote. We know that for a logarithmic function, $y={{\log }_{b}}\left( \text{argument} \right)$ , vertical asymptote is at $\text{argument}=0$ . Also, when a logarithmic function has its base in between 0 and 1, the graph will decrease from left to right. Then, we have to plot the graph using these data.

Complete step-by-step solution:
We have to graph $F\left( x \right)={{\log }_{\dfrac{1}{3}}}\left( x+5 \right)$ . Firstly, let us equate the RHS of this function to y.
$\Rightarrow y={{\log }_{\dfrac{1}{3}}}\left( x+5 \right)$
We have to find the x-intercept. We know that x-intercept occurs when $y=0$ .
$0={{\log }_{\dfrac{1}{3}}}\left( x+5 \right)$
We know that if ${{\log }_{b}}x=n$ , then ${{b}^{n}}=x$ . Therefore, we can write the above equation as
$\Rightarrow {{\left( \dfrac{1}{3} \right)}^{0}}=x+5$
We know that ${{a}^{0}}=1$ . Hence, we can write the above equation as
$\Rightarrow 1=x+5$
Let us find the value of x by taking 5 to the LHS.
$\begin{aligned} & \Rightarrow x=1-5 \\\ & \Rightarrow x=-4 \\\ \end{aligned}$
Hence, we obtained the x-intercept as $\left( -4,0 \right)$ .
Now, let us find the y-intercept by substituting $x=0$ .
$\begin{aligned} & \Rightarrow y={{\log }_{\dfrac{1}{3}}}\left( 0+5 \right) \\\ & \Rightarrow y={{\log }_{\dfrac{1}{3}}}5 \\\ \end{aligned}$
We know that ${{\log }_{b}}m=\dfrac{{{\log }_{a}}m}{{{\log }_{a}}b}$ . Let us consider the base, a, as 10. Therefore, the above equation becomes
$\Rightarrow y=\dfrac{\log 5}{\log \left( \dfrac{1}{3} \right)}$
We know that $\log \dfrac{a}{b}=\log a-\log b$ . Hence, we can write the above equation as
$\Rightarrow y=\dfrac{\log 5}{\log 1-\log 3}$
Let us substitute the values of the logarithms.
$\begin{aligned} & \Rightarrow y=\dfrac{0.698}{0-0.477} \\\ & \Rightarrow y=-\dfrac{0.698}{0.477} \\\ & \Rightarrow y=-1.463 \\\ \end{aligned}$
Hence, we obtained the y-intercept as $\left( 0,-1.463 \right)$ .
Now, let us find the vertical asymptote. For a logarithmic function $y={{\log }_{b}}\left( \text{argument} \right)$ , vertical asymptote is at $\text{argument}=0$ . Here, we can find the vertical asymptote as
$\begin{aligned} & \Rightarrow x+5=0 \\\ & \Rightarrow x=-5 \\\ \end{aligned}$
Therefore, vertical asymptote is at $x=-5$ .
We know that when a logarithmic function has its base less than one, the graph will be a decreasing logarithm. More clearly, we can state that if the base is between 0 and 1, the graph will decrease from left to right. Now, let us draw the graph using these data.

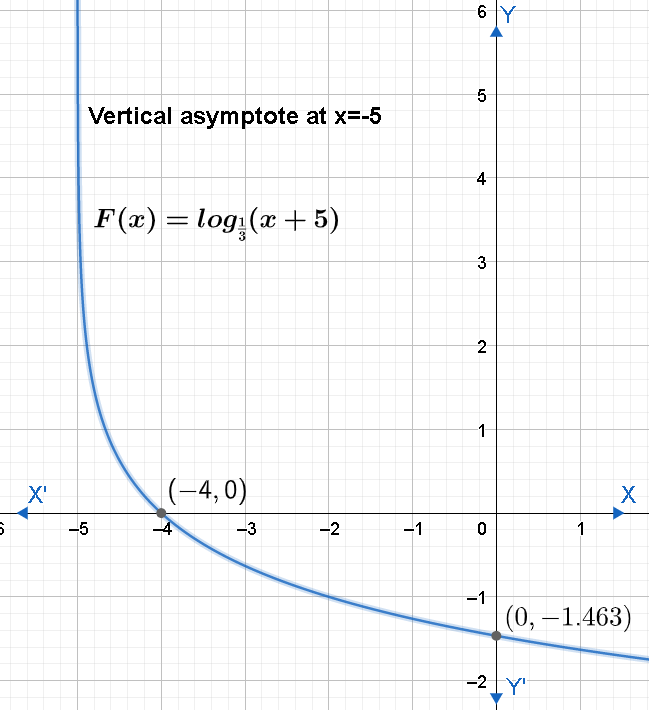
Note: Students must be thorough with the logarithm rules to find the solution of this question. They must know to find the asymptote of the logarithmic functions. Also note that logarithmic functions will never have horizontal asymptote. Students must know that we usually represent ${{\log }_{10}}$ as simply $\log$ . We can also find the graph of $y={{\log }_{\dfrac{1}{3}}}\left( x+5 \right)$ in an alternate way.
We can write the function $y={{\log }_{\dfrac{1}{3}}}\left( x+5 \right)$ as follows using the definition if ${{\log }_{b}}x=n$ , then ${{b}^{n}}=x$ .
$\Rightarrow {{\left( \dfrac{1}{3} \right)}^{y}}=x+5$
Now, let us take 5 to the LHS.
$\Rightarrow x={{\left( \dfrac{1}{3} \right)}^{y}}-5$
Now, we can substitute different values for y like -2, -1, 0, 1, 2 and find the corresponding values of x and draw the graph.