Question

How do you graph $f\left( x \right) = \ln x - 1$?

Answer 1

First draw a rough graph of $\ln x$ to understand the nature and shape of $\ln x - 1$. We know that the graph of $\ln x$ will be increasing throughout the positive $x -$axis from $- \infty$ at $x = 0$ to $\infty$ as $x \to \infty$. Then shift the graph of $\ln x$ downwards by 1 unit to get the correct graph of $\ln x - 1$.

Complete step-by-step solution:
According to the question, we have to show how to draw the graph of $f\left( x \right) = \ln x - 1$. For this, first we’ll draw the graph of $\ln x$ for reference to get the clear understanding of the nature and shape of $\ln x - 1$.
We know that the graph of $\ln x$ will be increasing throughout positive $x -$axis from $- \infty$ as $x \to 0$ to $\infty$ as $x \to \infty$ while having 1 as its value at $x = 0$. And $\ln x$ is defined for only positive $x$ so the graph will not have anything on the negative side of the $x -$axis. Based on these observations, the graph of $\ln x$ is as shown below:

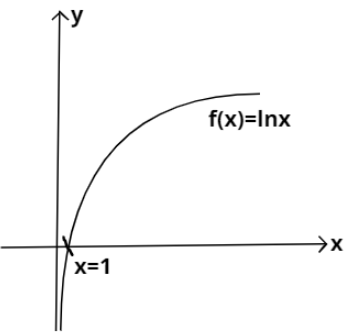
Now, for the graph of $\ln x - 1$, we will just shift the above graph of $\ln x$ downwards by 1 unit . For finding out the point where it cuts $x -$axis, we’ll put $\ln x - 1$ to zero. So we have:
$\Rightarrow \ln x - 1 = 0 \\\ \Rightarrow \ln x = 1 \\\ \Rightarrow x = e \\\$
So $\ln x - 1$ will cut the $x -$axis at $x = e$.
The graph of $f\left( x \right) = \ln x - 1$ is shown below:

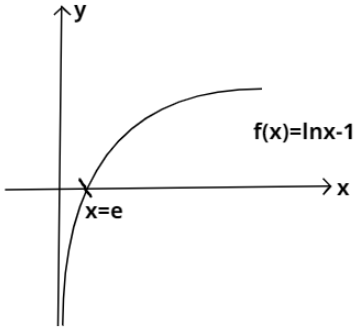
Note: If we know the graph of $y = f\left( x \right)$, then we can draw graphs related to this using the following rules:
(1) For the graph of $y = f\left( x \right) \pm a$, shift the graph of $y = f\left( x \right)$ by $a$ units upward or downward for positive and negative signs respectively.
(2) For the graph of $y = f\left( {x \pm a} \right)$, shift the graph of $y = f\left( x \right)$ by $a$ units left or right for positive and negative signs respectively.