Question

How do you graph $f\left( x \right) = {\left( {x + 2} \right)^2}?$

Answer 1

The given question describes the operation of addition/ subtraction/ multiplication/ division. Also, this problem involves the operation of substituting the $x$ values in the given equation to find $y$ values. Also, $y$ is the fraction of $x$. By using the values of $x$ and $y$ we can easily draw the graph. To make easy calculations we can simplify the given equation by using algebraic formulas.

Complete step by step solution:
The given question is shown below,
$y = f\left( x \right) = {\left( {x + 2} \right)^2} \to \left( 1 \right)$
We know that,
${\left( {a + b} \right)^2} = {a^2} + {b^2} + 2ab$
By using the above-mentioned algebraic formula we can simplify the equation $\left( 1 \right)$ as follows,
$\left( 1 \right) \to y = {\left( {x + 2} \right)^2}$

$$y = {x^2} + 2 \times 2 \times x + {2^2} \\\ y = {x^2} + 4x + 4 \to \left( 2 \right) \\\$$

We would draw the graph for the above equation.
As a first step, we would assume $x$ value as given below,
$x = ... - 2, - 1,0,1,2,.....$
By substituting the above-mentioned $x$ values in the equation $\left( 2 \right)$, we can find the $y$ values.
Let’s substitute $x = - 2$ in the equation $\left( 2 \right)$, we get
$\left( 2 \right) \to y = {x^2} + 4x + 4$

$$y = {\left( { - 2} \right)^2} + \left( {4 \times - 2} \right) + 4 \\\ y = 4 - 8 + 4 \\\ y = 0 \\\$$

Let’s substitute$x = - 1$ in the equation $\left( 2 \right)$, we get
$\left( 2 \right) \to y = {x^2} + 4x + 4$

$$y = {\left( { - 1} \right)^2} + 4\left( { - 1} \right) + 4 \\\ y = 1 - 4 + 4 \\\ y = 1 \\\$$

Let’s substitute $x = 0$ in the equation $\left( 2 \right)$, we get
$\left( 2 \right) \to y = {x^2} + 4x + 4$

$$y = {\left( 0 \right)^2} + 4\left( 0 \right) + 4 \\\ y = 4 \\\$$

Let’s substitute $x = 1$ in the equation $\left( 2 \right)$, we get
$\left( 2 \right) \to y = {x^2} + 4x + 4$

$$y = {\left( 1 \right)^2} + 4\left( 1 \right) + 4 \\\ y = 9 \\\$$

Let’s substitute $x = 2$ in the equation $\left( 2 \right)$, we get
$\left( 2 \right) \to y = {x^2} + 4x + 4$

$$y = {\left( 2 \right)^2} + \left( {4 \times 2} \right) + 2 \\\ y = 4 + 8 + 2 \\\ y = 14 \\\$$

Let’s make a tabular column by using the$x$and$y$values as given below,

$x$	$- 2$	$- 1$	$0$	$1$	$2$
$y$	$0$	$1$	$4$	$9$	$14$

By using these points we can easily draw the graph.

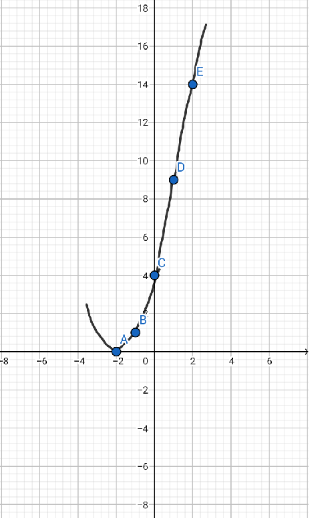
The above graph represents the equation $y\left( x \right) = {\left( {x + 2} \right)^2}$

Note: In this type of question we would assume $x$ value, by using the $x$ value we can find the value of $y$. The graph could be based on the equation. $y$ is the function of $x$. So, $y$ also can be written as $f\left( x \right)$. Note that $y = {x^2}$ the form equation always makes a parabolic shape in the graph sheet. Remember the algebraic formula ${\left( {a + b} \right)^2} = {a^2} + {b^2} + 2ab$.