Question

How do you graph $f\left( x \right)={{4}^{x}}+2$ by plotting points?

Answer 1

This question is from the topic of algebra. In this question, we will draw the graph of $f\left( x \right)={{4}^{x}}+2$. In solving this question, we will draw a table for about 11 values of x and using those values we will find the values of f(x). After using values of x and f(x), we will draw a graph putting the value of x along the x-axis and putting the values of f(x) along the y-axis.

Complete step-by-step answer:
Let us solve this question.
In this question, we have asked to draw the graph of given equation by plotting points. The given equation is
$f\left( x \right)={{4}^{x}}+2$
Let us put the values in place of x and find the values of x.
At x=-(infinity),
$f\left( -\infty \right)={{4}^{-\infty }}+2$
The above can also be written as
$\Rightarrow f\left( -\infty \right)=\dfrac{1}{{{4}^{\infty }}}+2$
As we know that ${{x}^{\infty }}=\infty$, where $x>1$
So, we can write
$\Rightarrow f\left( -\infty \right)=\dfrac{1}{\infty }+2$
As we know that inverse of infinity is zero, so we can write the above as
$\Rightarrow f\left( -\infty \right)=0+2=2$
Let us check at x=-4, we can write
$f\left( -4 \right)={{4}^{-4}}+2=0.003+2=2.003$
Now, let us check at x=-3, we can write
$f\left( -3 \right)={{4}^{-3}}+2=0.0156+2=2.0156$
Now, let us check at x=-2, we can write
$f\left( -2 \right)={{4}^{-2}}+2=0.0625+2=2.0625$
Now, let us check at x=-1, we can write
$f\left( -1 \right)={{4}^{-1}}+2=0.25+2=2.25$
Now, let us check at x=0, we can write
$f\left( 0 \right)={{4}^{0}}+2=1+2=3$
Now, let us check at x=1, we can write
$f\left( 1 \right)={{4}^{1}}+2=4+2=6$
Let us check at x=2, we can write
$f\left( 2 \right)={{4}^{2}}+2=16+2=18$
Now, let us check at x=infinity, we can write
$f\left( \infty \right)={{4}^{\infty }}+2$
As we know that ${{x}^{\infty }}=\infty$, where $x>1$, so we can write
$\Rightarrow f\left( \infty \right)=\infty +2$
As infinity is largest number, so if we add any number with infinity, it will be infinity.
$\Rightarrow f\left( \infty \right)=\infty$
Now, we will draw the on the above values that we have taken and found.

$x$	$-\infty$	-4	-3	-2	-1	0	1	2	$\infty$
$f\left( x \right)$	2	2.003	2.0156	2.0625	2.25	3	6	18	$\infty$

Now, we will draw the graph using this table, where we will take x along x-axis and take $f\left( x \right)$ along y-axis.

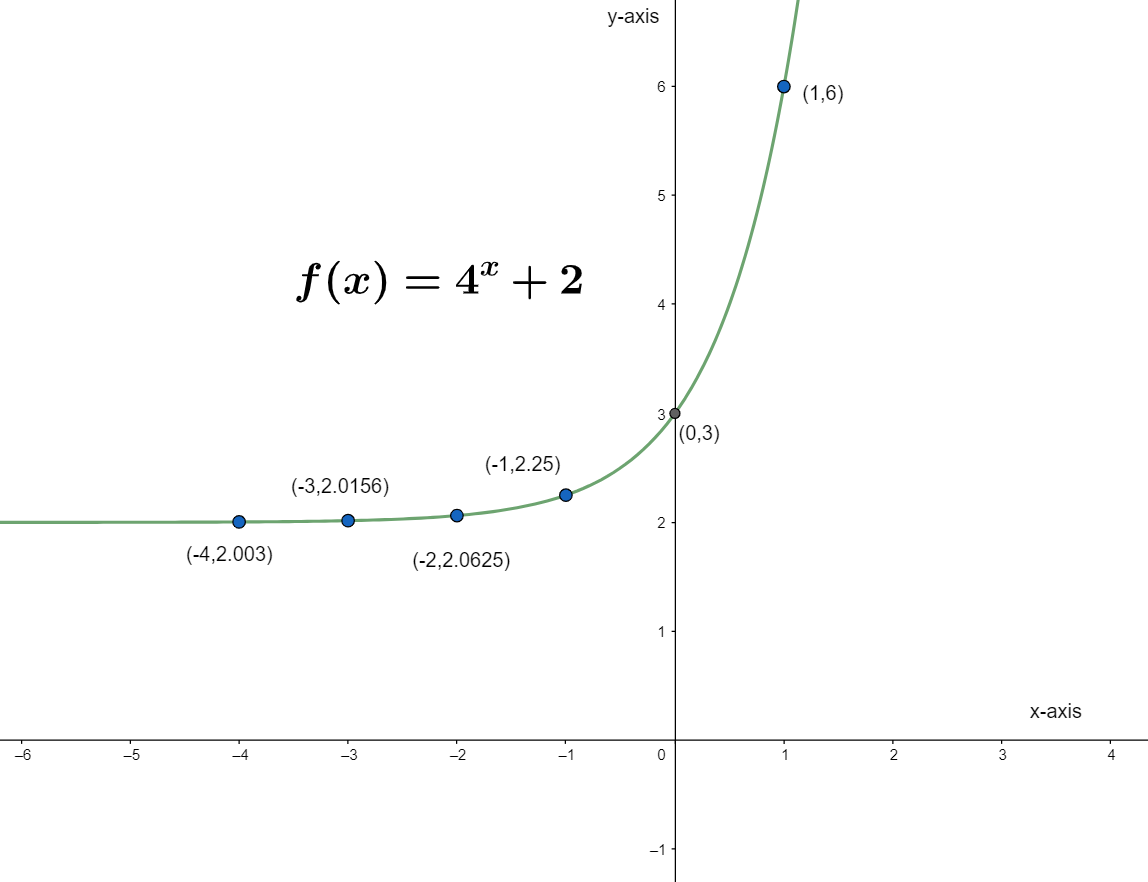
Here, we can see that at x=-(infinity), the graph is at y=2 and at x=infinity, the graph is going to infinity.
Hence, now we have drawn the graph of $f\left( x \right)={{4}^{x}}+2$ by plotting the points.

Note: As we can see that this question is from the topic of algebra, so we should have a better knowledge in that topic. We should know how to draw the graph of any equation by plotting the points.
Remember that:
${{x}^{\infty }}=\infty$, where $x>1$
${{x}^{-\infty }}=0$, where $x<1$
$\dfrac{1}{\infty }=0$