Question

How do you graph:-$f\left( x \right) = {4^x}$?

Answer 1

Plot a table first and make two columns and 5 rows. Now for every value of x starting from -2, try to get the value of y. After getting all the points, tabulate them and then graph each point on the graph. After doing this, connect all the lines to get the graph you need.

Complete step by step solution:
In order to draw the graph of the given function $f\left( x \right) = {4^x}$ the first thing we will need to do is draw a table where we will note down respective values of x and y.

x	y
-2	0.0625
-1	0.25
0	1
1	4
2	16

Now we will point each point on the graph
Scale of our graph is horizontal line = X axis. Vertical line=Y axis. And 1 block is of 1 unit x axis and 2 unit on y axis.
So let’s start with the first one where
x=-2 in $f(x)$, we get y=0.0625
This means the point will be -2 points away from y axis and 0.0625 units away from x axis

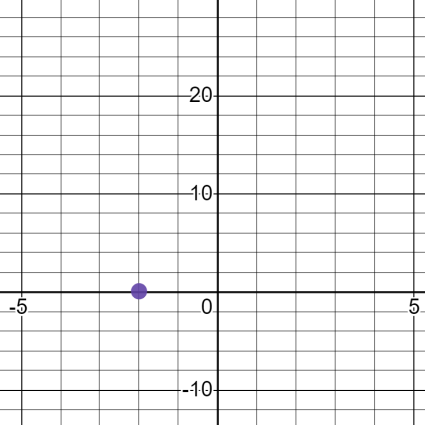
Now, we will graph the second point along with the first point
Where x=-1 in$f(x)$, we get y=0.25
This means the point will be -1 points away from y axis and 0.25 units away from x axis

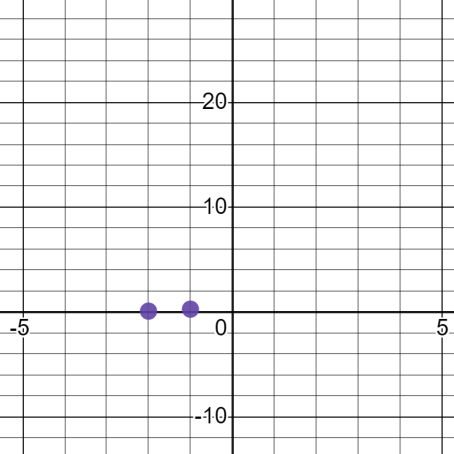
Now, we will graph the third point where
Where x=0 in$f(x)$, we get y=1
This means the point will be 0 points away from y axis and 1 units away from x axis

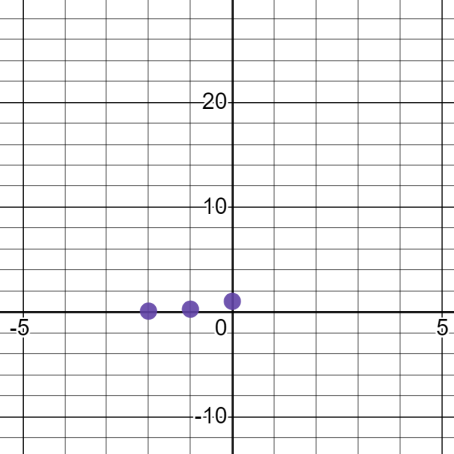
Now, we will graph the fourth point where
Where x=1 in$f(x)$, we get y=4
This means the point will be 1 points away from y axis and 4 units away from x axis

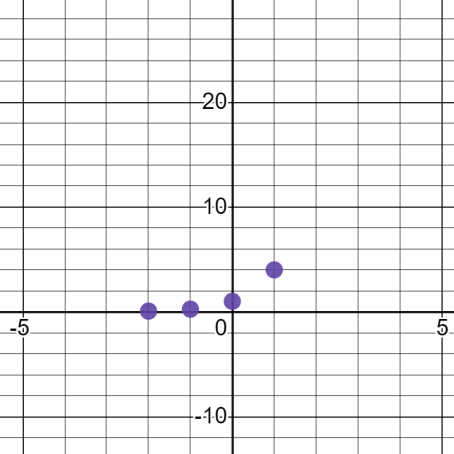
Now we will graph the fifth and last point where
Where x=2 in$f(x)$, we get y=16
This means the point will be 2 points away from y axis and 16 units away from x axis

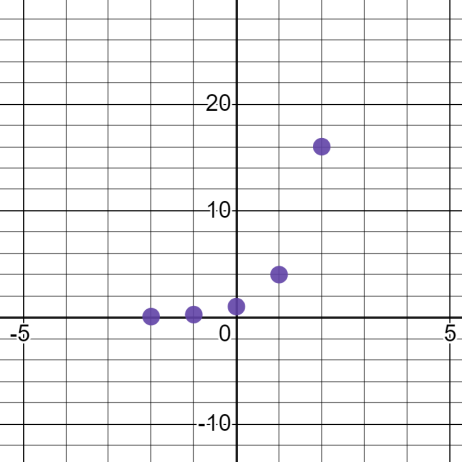
Now, the next step we will be needing to do is to plot this graph by connecting all the points that we have already drawn on the graph
So, after connecting everything, we will get:-

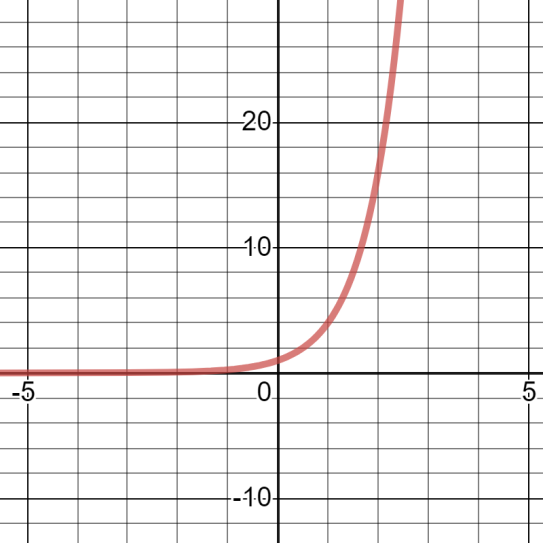
Note: Don't exchange the values of x or y. because the x value is for distance of a point from y axis and y value is for distance of a point from x axis. So (2,3) and (3,2) are totally different points. The distance from the axis and the value of the coordinate are of opposite signs ( X and Y ).