Question

How do you graph $f\left( x \right)=2x+1$ and then use the horizontal test to determine whether the inverse of $f\left( x \right)$ is a function?

Answer 1

We first explain the relation of inverse function with its function types. We find if the function is one-one or not. We use horizontal line tests to determine whether the inverse of $f\left( x \right)$ is a function and find the function if it exists.

Complete step-by-step solution:
We need to find whether the function $f\left( x \right)=2x+1$ has an inverse or not through a horizontal line test. If it has an inverse then we find the inverse.
First, we find the characteristics of the function $f\left( x \right)=2x+1$. It is a one-one function.
This means for a particular value of $x$, we will get only one value of $y$.
So, every value of $x$ can be projected to a particular value of $y$.
In case of one-one function, we can have an inverse always irrespective of the function.
In case many-one functions, we can’t have an inverse function.
Let’s assume that $g\left( a \right)=g\left( b \right)=c$ for an arbitrary function $g\left( x \right)$.
This is a two-one function. The domain has two values $a,b$ that give the same value of $c$ in range. Condition is $a\ne b$.
When we are taking the inverse, we get one value $c$ in domain which gives two values $a,b$ in range. That can’t be function as ${{g}^{-1}}\left( c \right)=a$ and ${{g}^{-1}}\left( c \right)=b$ but $a\ne b$.
The horizontal line test gives that for the function $f\left( x \right)$ if any horizontal line represented as $y=k$ on infinite extension cuts the graph more than once then the graph can’t have an inverse function.
For $f\left( x \right)=2x+1$, we have inverse function. Let $y=2x+1$ which gives $x=\dfrac{y-1}{2}$.
Therefore, the inverse function is ${{f}^{-1}}\left( x \right)=\dfrac{x-1}{2}$.
We take a horizontal line represented as $y=2$. We draw the graphs of $f\left( x \right)=2x+1$ and $y=2$.
We find their intersection.

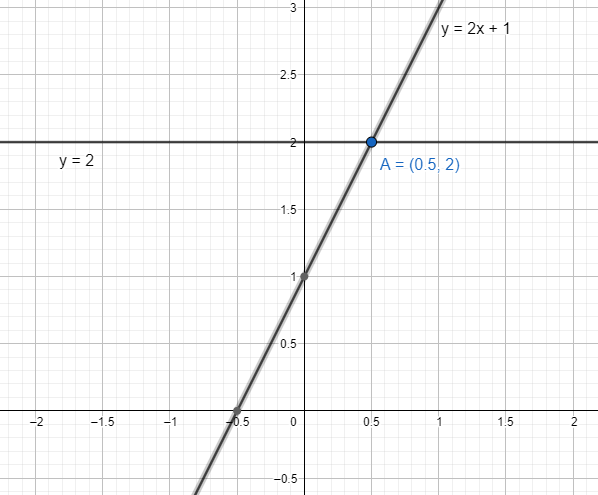
The only intersection is the point $A=\left( \dfrac{1}{2},2 \right)$. Therefore, the inverse of $f\left( x \right)$ exists.

Note: If the horizontal line intersects the graph of a function in all places at exactly one point, then the given function should have an inverse that is also a function. We say this function passes the horizontal line test.