Question

How do you graph $f\left( x \right)=2+\ln x$?

Answer 1

This question is from the topic of exponential and logistic graphs which belongs to the chapter pre-calculus. In this question, we will draw the graph of $f\left( x \right)=2+\ln x$. In solving this question, we will first find the values of $f\left( x \right)$ at x=0, 1, 2, 3, and $\infty$. After using these points and values of $f\left( x \right)$ at those points, we will draw the graph of the given equation.

Complete step by step solution:
Let us solve this question.
In this question, we have asked to find the graph of the equation which is given in the question. The given equation is $f\left( x \right)=2+\ln x$.
Let us first find out the value of $f\left( x \right)$ at x=0. We can write
$f\left( 0 \right)=2+\ln \left( 0 \right)$
As we know that the value of $\ln \left( 0 \right)$ is $-\infty$, so we can write
$\Rightarrow f\left( 0 \right)=2-\infty =-\infty$
Now, let us first find out the value of $f\left( x \right)$ at x=1. We can write
$f\left( 1 \right)=2+\ln \left( 1 \right)$
As we know that the value of $\ln \left( 1 \right)$ is 0, so we can write
$\Rightarrow f\left( 1 \right)=2+0=2$
Now, let us find out the value of $f\left( x \right)$ at x=2. We can write
$f\left( 2 \right)=2+\ln \left( 2 \right)$
As we know that the value of $\ln \left( 2 \right)$ is 0.693, so we can write
$\Rightarrow f\left( 2 \right)=2+0.693=2.693$
Now, let us find out the value of $f\left( x \right)$ at x=3.
$f\left( 3 \right)=2+\ln \left( 3 \right)$
Putting the value of $\ln \left( 3 \right)$ as 1.0986, we can write
$\Rightarrow f\left( 3 \right)=2+1.0986=3.0986$
Now, let us find the value of $f\left( x \right)$ at $x=\infty$.
$f\left( \infty \right)=2+\ln \left( \infty \right)$
Putting the value of $\ln \left( \infty \right)$ as $\infty$ in the above equation, we can write
$\Rightarrow f\left( \infty \right)=2+\infty =\infty$
Now, we have got the following values:

$x$	0	1	2	3	$\infty$
$f\left( x \right)$	$-\infty$	2	2.693	3.0986	$\infty$

Now, we will use the above table and draw the graph of $f\left( x \right)=2+\ln x$

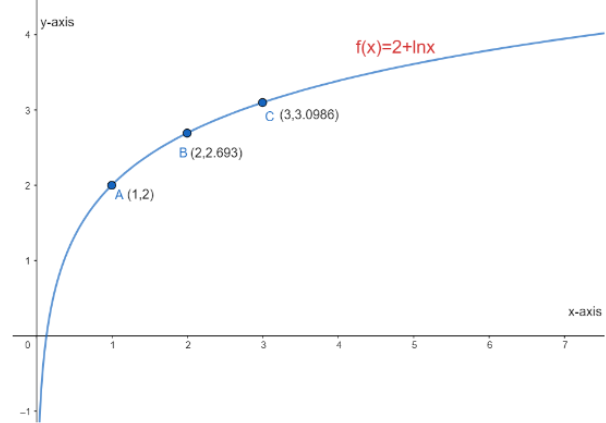
Now, we can see that at x=0, the value of f(x) is tending to negative or infinity at x equals to infinity, the value of f(x) is tending to infinity.

Note: We should have a better knowledge in the topic of exponential and logistic graphs to solve this type of question easily. We should remember the following values to solve this type of question easily:
Value of ‘e’ (that is exponential) = 2.71
$\ln 0=-\infty$
$\ln 1=0$
$\ln 2=0.693$
$\ln 3=1.0986$
$\ln \infty =\infty$
And, also remember that if $\ln x=y$, then $x={{e}^{y}}$