Question

How do you graph exponential function $f(x) = {3^x}$ ?

Answer 1

In this question, we have to plot a function in terms of two variables on the graph paper by plotting points. For graphing a function we have to find the coordinates of some of the points that can be plotted on the graph. We can let $f(x) = y$ , so by putting random values of one variable we can find the value of the other value from the given equation. Using this approach, we find out the coordinates of some points lying on the curve of the given exponential function and get the graph of the function by joining these points.

Complete step by step answer:
The given function is $f(x) = {3^x}$. As the function is equal to 3 raised to the power x, so x can take both positive and negative values but the value of the function will always come out to be positive. Thus, the graph will lie in the first and the second quadrant.
f(0) = {3^0} = 1 \\\ \Rightarrow f(1) = {3^1} = 3 \\\ \Rightarrow f(2) = {3^2} = 9 \\\ \Rightarrow f(3) = {3^3} = 27 \\\
So, the coordinates of some of the points in the first quadrant are $(0,1)$ , $(1,3)$ , $(2,9)$ and $(3,27)$ .So, the slope of the graph will be extremely steep in the first quadrant. To plot a proper graph of the given function, we need to consider its negative values also –
f( - 1) = {3^{ - 1}} = \dfrac{1}{3} \\\ \Rightarrow f( - 2) = {3^{ - 2}} = \dfrac{1}{9} \\\ \Rightarrow f( - 3) = {3^{ - 3}} = \dfrac{1}{{27}} \\\
So, the coordinates of some of the points in the second quadrant are $( - 1,\dfrac{1}{3})$ , $( - 2,\dfrac{1}{9})$ and $( - 3,\dfrac{1}{{27}})$ .So, the slope of the graph in the second quadrant will be near to zero.Joining all these points and extending the obtained curve, we can trace the graph of the function $f(x) = {3^x}$ .

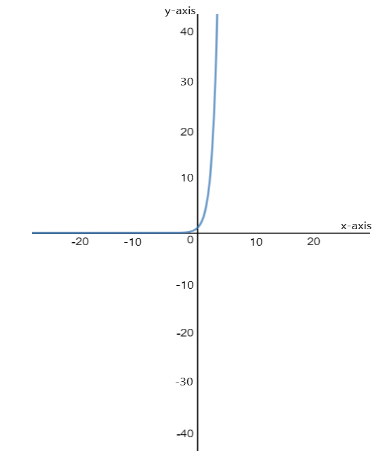
Note: We use a graph to study the relation between two variable quantities, a graph contains two axes that are perpendicular to each other namely the x-axis and the y-axis. The exponential functions increase rapidly as we increase the value of x. On pitting negative values of x, we see that the value of the function comes out to be very small and as we increase the magnitude of negative values, the answer gets closer and closer to zero.