Solveeit Logo
Login

Question

Question: How do you graph \(\dfrac{{{x^2} - 4}}{{{x^2} - 9}}\)?...

How do you graph x2−4x2−9\dfrac{{{x^2} - 4}}{{{x^2} - 9}}?

Explanation

Solution

Find intercepts and asymptotes and then plot the graph.
First, we are going to find the x-intercept and then we are going to the y-intercept of the given expression, after we find that then we are going to find the vertical asymptotes and then the horizontal asymptotes, then we are clear to plot the graph accordingly in the left region, right regions and also the middle region of the graph.

Complete step by step answer:
First, we Find the y-intercepts.
y=f(x)=x2−4x2−9 f(0)=0−40−9=−4−9=49  y = f(x) = \dfrac{{{x^2} - 4}}{{{x^2} - 9}} \\\ f(0) = \dfrac{{0 - 4}}{{0 - 9}} = \dfrac{{ - 4}}{{ - 9}} = \dfrac{4}{9} \\\
We have the y-intercepts now which are (0,49)(0,\dfrac{4}{9}).
Now, we are going to find the x-intercepts

0=x2−4x2−9 x2−4=0 x2=4 x=±2  0 = \dfrac{{{x^2} - 4}}{{{x^2} - 9}} \\\ {x^2} - 4 = 0 \\\ {x^2} = 4 \\\ x = \pm 2 \\\

Therefore, the x-intercepts are (−2,0) and (2,0)( - 2,0){\text{ }}and{\text{ }}(2,0).
Now, next we have to find the asymptotes of the expression.
So, we find the vertical asymptotes
We can find it by setting the denominator equal to zero and solve for x.

x2−9=0 x2=9 x=±3  {x^2} - 9 = 0 \\\ {x^2} = 9 \\\ x = \pm 3 \\\

There are vertical asymptotes at x=−3x = - 3 and x=3x = 3.
Next, we have to find the horizontal asymptotes
Since both the equations are of order 2, we divide the coefficients of x2{x^2} terms.
11=1\dfrac{1}{1} = 1
The horizontal asymptote is at y=1y = 1.

Now, we can begin plotting the graph by first drawing the asymptotes

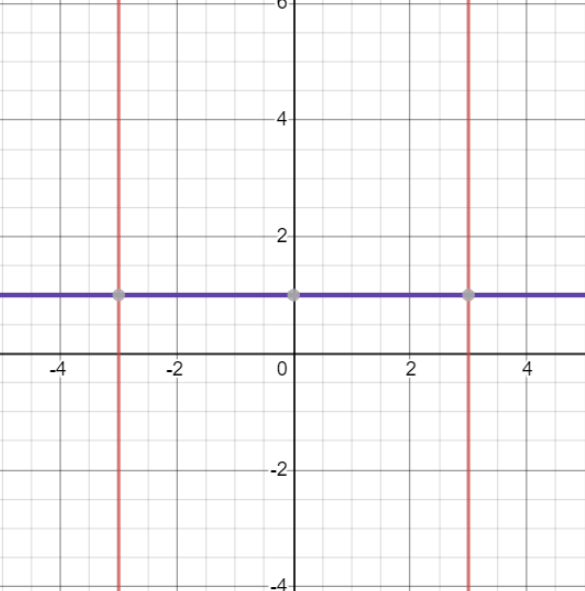
We can see that the vertical asymptotes divide the graph into three regions (left, right and middle)
In the left region,
f(−4)=16−416−9=127≈1.7f( - 4) = \dfrac{{16 - 4}}{{16 - 9}} = \dfrac{{12}}{7} \approx 1.7
The point (−4,1.7)( - 4,1.7) lies in the second quadrant.

In the right region,
f(4)=16−416−9=127≈1.7f(4) = \dfrac{{16 - 4}}{{16 - 9}} = \dfrac{{12}}{7} \approx 1.7
We have a mirror image in the first quadrant like that of the second quadrant
In the middle region,
f(0)=49≈0.44f(0) = \dfrac{4}{9} \approx 0.44 and
f(−1)=f(1)=1−41−9=−3−8≈0.38f( - 1) = f(1) = \dfrac{{1 - 4}}{{1 - 9}} = \dfrac{{ - 3}}{{ - 8}} \approx 0.38
The points at (−1,0.38)\left( { - 1,0.38} \right)and (1,0.38)\left( {1,0.38} \right) are below the y-intercept.

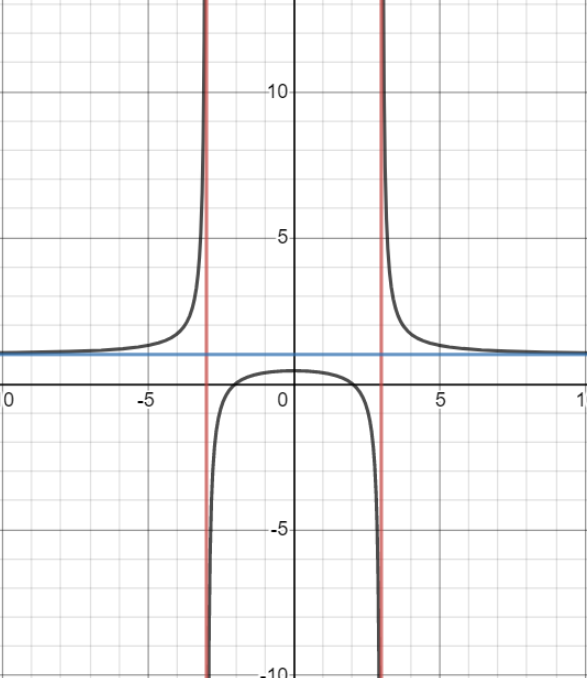
The above is the graph of the given expression.

Note: For the middle region, we have to take two different values, as it touches two different quadrants and which forms complete inverted parabola. While finding the intercepts we have been careful will nullifying a variable.