Question

How do you graph $\dfrac{\cos x}{x}$?

Answer 1

To draw the graph of the given function we will first analyze the function on different points. Hence we will find the endpoint behavior and the points on which the function is not defined. Also we will check the roots of the function. Hence we will try to draw the graph of the function.

Complete step-by-step solution:
Let us first consider the given function.
Now the given function is nothing but $f\left( x \right)=\cos x\times \dfrac{1}{x}$. Hence the function will be a hybrid of both the functions $\cos x$ and $\dfrac{1}{x}$.
Now first we know that the function $f\left( x \right)=\cos x\times \dfrac{1}{x}$ will not be defined at x = 0 since the denominator can never be 0.
Hence as x tends to zero the value of the function tends to infinity.
Also since $\cos \left( 0 \right)=1>0$ we can say x tends to zero from the positive side we will get positive infinity and as x tends to 0 from the negative side we will get negative infinity.
Now note that also as x tends to infinity the function approaches the value of 0.
Now the roots of the function $f\left( x \right)=\cos x\times \dfrac{1}{x}$ will be same as the roots of the function $\cos x$
Hence we will have multiple roots of the given function.
Now we know that $-1\le \cos x\le 1$.
Hence we have $\dfrac{-1}{x}\le \dfrac{\cos x}{x}\le \dfrac{1}{x}$
Hence we can say that the value of the function will be greater than 1 for x less than 1 and the value of the function will be less than 1 for x greater than 1.
Hence the given function will look like,

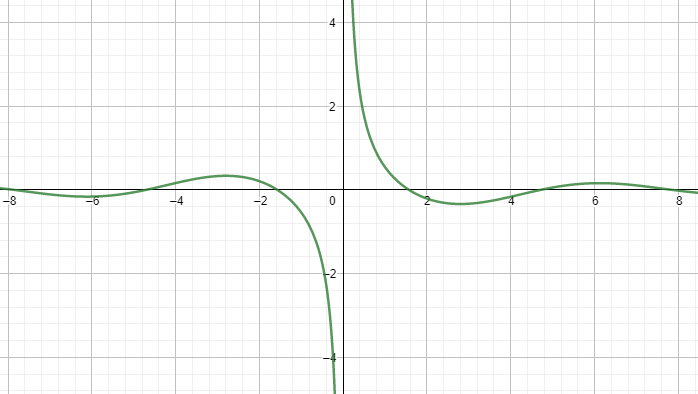
Note: Now note that here the function $\dfrac{\cos x}{x}$ looks a lot like the function $\dfrac{1}{x}$. Though this is not always true. The resultant graph of a product of two functions can be a completely new graph itself. Also note that cosx is an even function and $\dfrac{1}{x}$ is an odd function and the multiplication gives us an odd function.