Question

How do you graph and solve $\left| {4x + 8} \right| \geqslant 20$?

Answer 1

To solve the given question, we will first find out the absolute value. After that, we will solve this linear inequality by taking positive and negative values. From these values, we will get the intervals. Finally, we get two points and also plot these two points on the graph.

Complete step-by-step answer:
In this question, we want to solve $\left| {4x + 8} \right| \geqslant 20$.
As we already know that, $\left| {4x + 8} \right|$ have two values as follow:
The first value is $\left| {4x + 8} \right|$=$4x + 8$if$\left| {4x + 8} \right| \geqslant 0$.
And, the second value is $\left| {4x + 8} \right|$=$- \left( {4x + 8} \right)$ if$\left| {4x + 8} \right| < 0$.
To find the absolute value, let us take $4x + 8 = 0$
Let us subtract the above equation by -8 on both sides.
$\Rightarrow 4x + 8 - 8 = 0 - 8$
So,
$\Rightarrow 4x = - 8$
Now, let us divide the above equation by 4 into both sides.
$\Rightarrow \dfrac{{4x}}{4} = \dfrac{{ - 8}}{4}$
So,
$\Rightarrow x = - 2$
So, the value of the term $4x + 8$ changes from negative to positive at the point $x = - 2$.
In the first case,
$\Rightarrow \left| {4x + 8} \right| \geqslant 0$
Therefore,
$\Rightarrow \left| {4x + 8} \right|$=$4x + 8$
Here, our initial identity is below:
$\Rightarrow 4x + 8 \geqslant 20$
Let us subtract the above equation by -8 on both sides.
$\Rightarrow 4x + 8 - 8 \geqslant 20 - 8$
So,
$\Rightarrow 4x \geqslant 12$
Now, let us divide the above equation by 4 into both sides.
$\Rightarrow \dfrac{{4x}}{4} \geqslant \dfrac{{12}}{4}$
So,
$\Rightarrow x \geqslant 3$
Hence, the interval is from $x \leqslant - 2$to$x \geqslant 3$
In the second case,
$\Rightarrow \left| {4x + 8} \right| < 0$
Therefore,
$\Rightarrow \left| {4x + 8} \right|$=$- \left( {4x + 8} \right)$
That is equal to,
$\Rightarrow \left| {4x + 8} \right| = - 4x - 8$
Here, our initial identity is below:
$\Rightarrow - 4x - 8 \geqslant 20$
Let us subtract the above equation by 8 on both sides.
$\Rightarrow - 4x - 8 + 8 \geqslant 20 + 8$
So,
$\Rightarrow - 4x \geqslant 28$
Now, let us divide the above equation by 4 into both sides.
$\Rightarrow - \dfrac{{4x}}{4} \geqslant \dfrac{{28}}{4}$
So,
$\Rightarrow - x \geqslant 7$
That is equal to,
$\Rightarrow x \leqslant - 7$
Hence, the interval is from $x \leqslant - 7$ to $x \leqslant - 2$.
Here, we have two separate intervals that represent the solutions to this inequality $x \leqslant - 7$ and $x \geqslant 3$.

Now, let us plot these points on the graph.

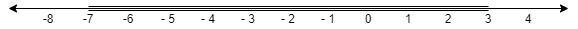
Note:
Linear inequality: In mathematics, a linear inequality is an inequality that involves a linear function. It contains the inequality symbols like $< , > , \leqslant , \geqslant , = , \ne$. It shows data that is not equal in graph form. It requires well-defined operations of addition, multiplication, and comparison.